集合的运算定律jihe de yunsuan dinglu

指下列集合运算所具有的性质.
❶交换律 A∪B=B∪A;A∩B=B∩A.

❷结合律 A∪(B∪C)=(A∪B)∪C;
A∩(B∩C)=(A∩B)∩C.

❸分配律

A∩(B∪C)=(A∩B)

∪(A∩C)，交对并的分配律；A∪(B∩C)=(A∪B)
∩(A∪C)，并对交的分配律.

❹德·莫根律A\\(B∪C)=(A\\B)∩(A\\C),
　A\\(B∩C)=(A\\B)∪(A\\C),
以上两个性质称为差的德·莫根律；

以上两个性质称为补的德·莫根律.

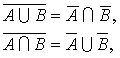
❺等幂律 A∪A=A;
A∩A=A.

❻吸收律 A∪(A∩B)=A; A∩(A∪B)=A.

❼求补律（互余律）A∪A=I;
　A∩A=Φ.

❽对合律(重非律、复原律) A=A.
此外，集合的运算还有以下一些性质：
❶A∪I=I;
❷A∩I=A;
❸A∪Φ=A;
❹A∩Φ=Φ;
❺I=Φ;
❻Φ=I.