隐函数的求导法
隐函数的求导法yinhamshu de qiudaofa
若y=f (x)是由方程F(x,y)=0确定的可导函数,则这个隐函数的导数f′ (x)可由方程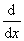 F (x,f (x))=0求得。
F (x,f (x))=0求得。
因为由F (x,y)=0确定的函数y=f (x)使F (x,f (x)) =0成为关于x的恒等式,所以,恒等式两边关于x的导数相等,并且可以表示成含x,y,y′ 的方程。解这个方程,便可求出y′ =f′ (x)。这种方法称为隐函数求导法。
例如,可用隐函数求导法求过双曲线 上一点 (x0,y0) (y0≠0)的切线方程。
上一点 (x0,y0) (y0≠0)的切线方程。
设过点(x0,y0)的切线斜率为k。将y看成x的函数,将方程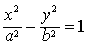 两边同时对x求导,得
两边同时对x求导,得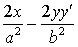 =0。解得
=0。解得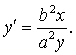 。在点 (x0,y0)处的切线斜率为k
。在点 (x0,y0)处的切线斜率为k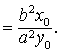 是,切线方程是
是,切线方程是
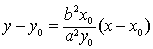
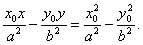 因为点 (x0,y0)在双曲线上,所以
因为点 (x0,y0)在双曲线上,所以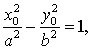 ,所求的切线方程为
,所求的切线方程为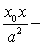
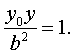
☚ 由参数方程所确定的函数的求导法则 对数求导法 ☛
- 中印边界秘史是什么意思
- 中印边界自卫反击战是什么意思
- 中印边界自卫反击战是什么意思
- 中印边界问题是什么意思
- 中印边界问题是什么意思
- 中印边界问题是什么意思
- 中印边界问题(三)是什么意思
- 中印边界问题(二)是什么意思
- 中厄友好条约是什么意思
- 中压可调节型衬四氟蝶阀是什么意思
- 中厚板理论是什么意思
- 中原是什么意思
- 中原是什么意思
- 中原是什么意思
- 中原中也是什么意思
- 中原书市是什么意思
- 中原乱,簪缨散,几时收是什么意思
- 中原事,纵匈奴未灭,毕竟男儿是什么意思
- 中原人民抗契丹之战是什么意思
- 中原人民抗辽是什么意思
- 中原人民抗金之战是什么意思
- 中原会师是什么意思
- 中原初逐鹿,投笔事戎轩。纵横计不就,慷慨志犹存是什么意思
- 中原剧社是什么意思
- 中原地古多劲草,节如箭竹花如稻。白露洒叶珠离离,十月霜风吹不倒。是什么意思
- 中原声韵是什么意思
- 中原大地是什么意思
- 中原大战是什么意思
- 中原报是什么意思
- 中原敌后风云是什么意思
- 中原日报是什么意思
- 中原暴动是什么意思
- 中原村惨案是什么意思
- 中原画报是什么意思
- 中原突围是什么意思
- 中原突围是什么意思
- 中原突围是什么意思
- 中原突围时复员隐蔽和掉队人员的历史遗留问题是什么意思
- 中原突围纪事是什么意思
- 中原经济技术协作区是什么意思
- 中原英烈(上)是什么意思
- 中原血是什么意思
- 中原解放军北路突围与豫鄂陕革命根据地是什么意思
- 中原豪侠传是什么意思
- 中原远古文化是什么意思
- 中原逐鹿是什么意思
- 中原逐鹿是什么意思
- 中原逐鹿是什么意思
- 中原逐鹿是什么意思
- 中原逐鹿是什么意思
- 中原雅音是什么意思
- 中原雅音是什么意思
- 中原雅音研究是什么意思
- 中原雅音研究是什么意思
- 中原音韵是什么意思
- 中原音韵是什么意思
- 中原音韵是什么意思
- 中原音韵是什么意思
- 中原音韵是什么意思
- 中原音韵是什么意思