刚体的平面运动

---

刚体上各点到某一固定平面的距离保持不变的运动称为平面运动。这种运动可简化成刚体上与固定平面平行的截面图形在它所在的平面上的运动。

2．5．1 研究刚体平面运动的两种方法

纯滚动法：刚体作平面运动时，其上速度为零的点称为瞬时速度中心，简称瞬心。瞬心在固定空间描出的曲线称为空间极迹，瞬心在刚体上描出的曲线称为本体极迹。刚体的运动可视为刚体的本体极迹在其空间极迹上的纯滚动(见图1．2－10)。如轨道上行驶的车轮，轨道曲线即为空间极迹，车轮的轮缘曲线即为本体极迹。

基点法(运动分解法)：在平面图形上任取一点Ο′(称为基点)，建立平动坐标系Ο′x′y′，则平面图形的运动可分解为随Ο′点的牵连平动和相对于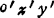的定轴转动，见图1．2－11，即

(刚体平而运动)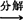(平 动)+(定轴转动)

(绝对运动) (牵连运动)(相对运动)

显然，刚体的瞬时位置可由Ο′的绝对坐标(x₀′，y。′)和图形上直线o′A的方位角φ来确定，即

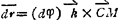
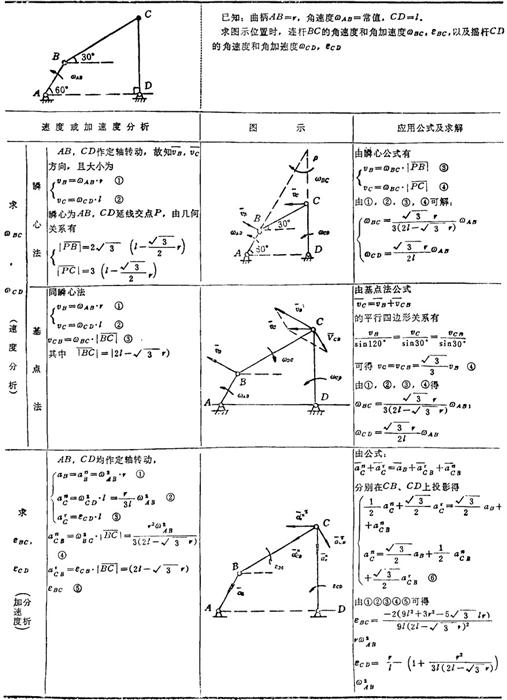
式中 C为△t→0(即dt)时，图形转动中心的位置。显然，亦为图形的速度瞬心位置。将其两边同除dt。即得M点的速度为