分式

---

整式A除以整式B，可以表示成A/B的形式，如果除式B中含有字母，那么称A/B为分式，其中A称为分式的分子，B称为分式的分母，对于任意一个分式，分母都不能为零．

注意 1．分式是两个整式相除的商式，其中分子是被除式，分母是除式，分数线起除号的作用，另外还有括号作用．

2．分式的分母中必须含有字母，而分子中可以含有字母，也可以不含有字母．

3．分式有意义的前提条件是分母必须不为零．

4．分式的值为零必须同时满足两个条件：一是分母不为零；二是分子为零．

5．当分子、分母同号时，分式的值为正；当分子、分母异号时，分式的值为负．

例1 把下列各代数式填在相应的大括号内：

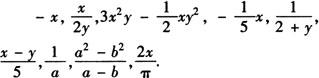
❶ 整式的集合{ …}；

❷ 分式的集合{ …}．

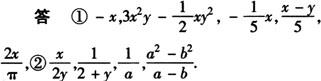
[解析] ❶ 判断一个代数式是否是分式，关键看分母中是否有字母，如果有字母，就是分式，不用看化简后的结果，比如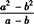=a+b，但原形式仍是分式．

❷ π是一个数，而不是字母．

例2 当x为何值时，下列分式有意义：

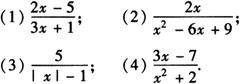
解 (1)当分母3x+1=0时，x=－1/3，所以x≠－1/3时，分式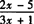有意义．

(2)当分母x²－6x+9=0，即(x－3)²=0时，x=3，所以当x≠3时，分式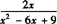有意义．

(3)当分母|x|－1=0时，x=±1，所以当x≠±1时，分式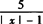有意义．

(4)因为x²≥0所以x²+2>0，不论x取任何实数，分母不可能为零，所以不论x取何值，分式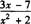都有意义．

[解析] 判断一个分式是否有意义，关键是看分母，只要分母不为零，则分式有意义，若分母为零则分式无意义．