函数极限的四则运算

---

这些法则对于x→∞(x→x₀⁺，x→x₀^—，x→+∞，x→—∞)的情况仍然成立．

例1 求下列函数的极限：

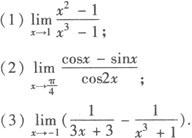
解 以上各题所求极限，均属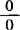或∞—∞型，需进行恒等变形约去“0”因子，或化为可进行四则运算的极限．

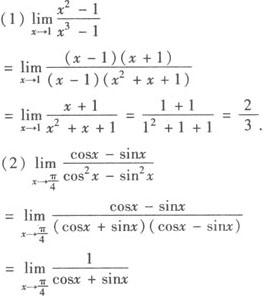
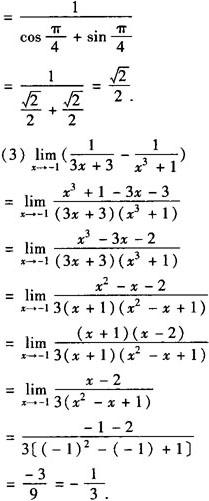
例2 设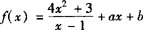，求分别满足(1)
❶ ，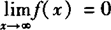
❷ 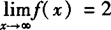的实数a，b的值，(2)讨论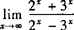的值的情况．

解 对于“”“∞—∞”型的极限，不能直接运用函数极限四则运算法则需先恒等变形，然后再进行四则运算．

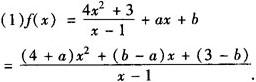
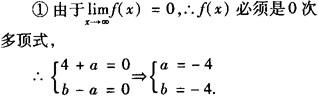
在数列极限中n→∞只表示n→+∞，在函数极限中n→∞表示，n→+∞和n→—∞两种变化趋势，故在研究或讨论“x→∞时，f(x)的极限”时需分别讨论x→+∞和x→—∞两种变化趋势下的f(x)的极限．

例3 求函数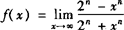的定义域并画出其图象．

解 当|x|<2时，

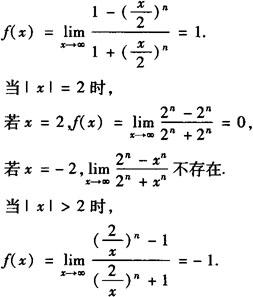
由此可见，f(x)定义域为{x|x≠—2，x∈R}

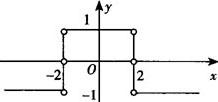
图象如下：