函数y=Asin(ωx+φ)的图象

---

❶ “五点法”作y=Asin(ωx+φ)(A>0，ω>0)简图．令X=ωx+φ，由X取0、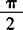、π、3/2π、2π求相应的x及对应的y值，再描点作图．

❷ 利用图象变换法作y=Asin(ωx+φ)(A>0，ω>0)简图．

a．振幅变换y=sinx→y=Asinx

将y=sinx的图象上各点的纵坐标变为原来的A倍(横坐标不变)．

b．相位变换：y=Asinx→y=Asin(x+φ)

将y=Asinx的图象上所有点向左(φ>0)或向右(φ<0)平移|φ|个单位．

c．周期变换：y=sin(x+φ)→y=Asin(ωx+φ)．

将y=sin(x+φ)的图象上各点的横坐标变为原来的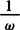倍(纵坐标不变)．

注 如果先作周期的变换，后作相位的变换，则左右平移时不是|φ|个单位，而是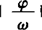个单位，即y=sin(ωx)→y=sin(ωx+φ)是左右平移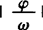个单位长度．

❸ A、ω、φ的物理意义．

当函数y=sin(ωx+φ)(A>0，ω>0，x∈(0，+∞))表示一个振动量时，A叫做振幅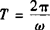，叫做周期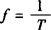，叫做频率，ωx+φ叫做相位，φ叫做初相．

例 已知函数y=Asin(ωx+φ)(A>0，ω>0)．

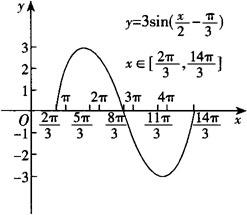
(1)若A=3，ω=1/2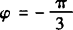，，作出该函数在一个周期内的草图；

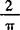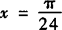(2)若y表示一个振动量，其振动频率为，当时，相位为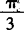，求ω与φ．

解 (1)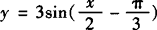，列出下表

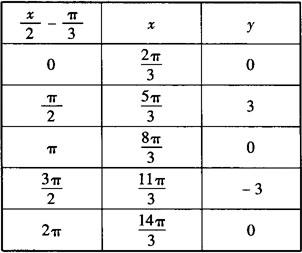
描出对应五点(x，y)，

用光滑曲线连结各点即得所应做的函数图象．