适合性检验shihexing jianyan

是检验样本的实际分布F_n(X)与总体某种分类准则的分布F(X)是否适应或一致。若样本来自某种分类的总体，则样本的实际分布F_n(X)与总体分布F(X)应有一定程度的吻合。设按某种分类准则把变量X的所有可能值分成K类或K个没有公共点的组，每组的理论频率为P_i，则样本中相应各组的理论次数f_e为NPi(N为样本总次数)；若样本中各组的实际观测次数f₀＝ni，则依X2分布中的结论有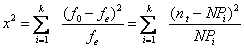

它服从于自由度为K-1的X2分布。显然，若样本实际分布Fn(X)适合总体分布F(X)，则fo与fe的差异就小，X²值也较小；否则，fo与fe的差异就较大，X2值也增大。当X²值大到一定界限后，我们就拒绝样本分布适合总体分布的假设。
[例1] 某市中学教师队伍老、中、青的比例为2:5:3，该市某中学的老年教师27人、中年教师43人、青年教师20人。问该校教师队伍的结构比例与全市情况是否一致？
本例中把某市中学教师队伍的老、中、青的比例看成总体某种分类准则的分布，把该校看成一个样本，在样本中也进行这种分类。因此检验的假设H₀为：该校教师队伍的结构比例与全市的情况一致。显然，在总体中P₁＝0.2、P₂＝0.5、P₃＝0.3，在样本中n₁＝27、n₂

据自由度f=K-1=3-1=2及α=0.05查X2分布表得X2_(2)0.05＝5.99；由于X²>X(₂₎₂₀.₀₅，故拒绝H₀。
注意：当K=2且其中有一组的fc=NP_i<10时，要用下式的“连续校正法”计X²值：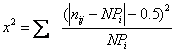

我们可据上述公式对各种分布进行适合性检验。第一式常用来检验某分布是否服从正态。
[例2] 据“理解水平测验”结果把某中学初一级488名学生分成Ⅰ、Ⅱ、Ⅲ级水平，这3级水平的人数分别为98,307,83。问它们是否服从正态分布？
设立假设H₀:这3种水平的人数分布服从正态分布。
这里的关键是求出正态分布下各水平所占的面积（概率）Pi，然后依fc=NP_i而计出各水平的理论次数。为此，我们把正态分布下的基线长6σ(一般由-3σ～3σ)进行3等分(每等分为2σ)，据此在正态分布表中查到它们的面积Pi。即

水平	范 围	概 率 (P)	理论人数 (NPi)	实际人数 (ni)
Ⅰ	-3σ～-1σ	0.16	78	98
Ⅱ	-1σ～1σ	0.68	332	307
Ⅲ	1σ～3σ	0.16	78	83

依式计得X²＝7.331，依f=3-1=2及α=0.05查X²分布表得：X(₂)₀.₀₅＝5.991，由X²>X(₂)₀.₀₅，故拒绝H₀。
若样本的数据已分组，采用下列步骤检验H0:样本的分布服从于正态分布。
❶求样本的平均数()与标准差(S)。

❷计每组在正态分布下的理论次数f_c。
首先，依下式求各组在正态分布下的概率Pi
…，K)
X_i——各组的上限。
其次，求理论次数ff=NP_i

❸计X2值，作统计检验。
[例3]检验某中学化学高考分数是否符合正态分布。
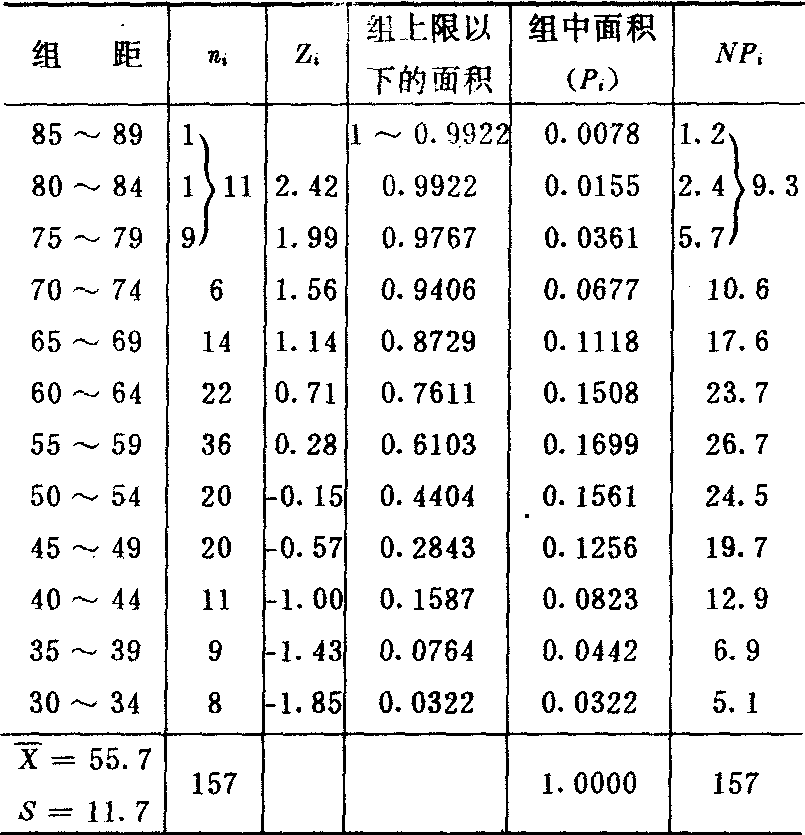
H0:某中学的化学高考分数符合正态分布。其计算过程列表如下：

注意：
❶每组的理论数fc≥5。若fc<5时，则必须与邻近的组合并直至使每组的fc≥5。上例中第1、2组合并后f_c尚小于5，故还必须与第3组合并，使f_c＝9.3>5为止。
❷K是合并后的组数。
❸自由度f=K-3，是由于在标准分数中使用了平均数和标准差，便失去了2个自由度，加上原来失的1个，故共失去了3个自由度。
f=10-3=7及α=0.05查X²分布表得X2(7)₀.₀₅＝14.067。由于X205，故接受H₀，即认为样本来自正态分布的总体。