连通

相通

通（连通） 达 洪同 相经
事情相通：同条共贯
与四面相通：四达
连接相通：贯(贯串；贯通；贯穿；贯达；贯穴；贯轶；贯统；连贯；联贯；横～) 穿(～通；～透；穿连) 关(关穿；关通) 通连 连通 交通 疏通 逾延 控引
贯通南北：纵贯 通南彻北
贯通上下：彻上彻下
会合贯通：洞同
纵横贯通：交通(～阡陌)
间杂，贯串：参贯
通到骨头：彻骨
(事物之间彼此连贯沟通：相通)

另见：阻塞 阻隔 开通

---

相连

比（邻比） 相属 连接 交结 盘牙 盘互 穿连 毗连 边带
互相连接或接连不断：贝联珠贯
两物相连：连二
形体相连：连形
粘连或互相连接：粘(～上；～附)
与天相连：连天
仿佛与天连接：黏天
山水光焰等与天连接：连天(芳草～)
如云霞相连：霞连
依次相连：连第
并连相接：軿接
条条相连：缕缕(炊烟～) 丝丝(冷雨～)
前后相连：接榫 衔接 衔尾 尾衔 继踵 接踵(～而出) 连络 交头 首尾相接
足踵相接，相继：相踵
交会相连：错连 襟连
交错相连：管络 婵媛
相通连接：贯(贯穿；贯通；贯连；穿贯)串通 连通 通连 关通
将一种理论、思想贯穿于事物的始终：一以贯之 一理贯之 以一贯之
相连成片：连片 连畛 连轸 连疆 连成一片
地方连片：连地
田地连片：连陌 连塍 连畴接陇
紧密相连：密接 连璅
密接无空隙：紧凑 紧峭 无间
两种事物紧密相连：响答影随 响和景从
相隔极短，紧相连接：节节寸寸
相连的样子：骈衍 骈然 婵嫣 迤迤 猎捷 迤靡 踟蹰 绎绎 迤迤 迤靡 离离 虹洞 隐隐展展
相连不绝的样子：丽靡
(互相连接：相连)

连通liantong

无向图G中，若点u,v之间存在路，则称u,v是连通的.若无向图G的任意二点都是连通的，则G称为连通图.
若认为无向图G的任意点“自身是连通的，则无向图G中点的连通关系是点集的一个等价关系，即适合自反性、对称性、传递性的关系. 于是，G的点集V能划分成互不相交的子集V₁,V₂，…，V_k的并； V₁ ∪V₂ ∪…∪V_k＝V,i≠j,V_i∩V_j＝φ.不同的V_i,V_j，中的点互不连通，而同一V_i中的点彼此连通.每个V _i的点及它们关联的边构成G的子图G_i，称为G的一个连通分支； W (G) =k称为G的连通分支数，当W (G)=1时，称G是连通图.
无向连通图的这两个定义是等价的.
对于有向图G来说，若存在u到v的有向路，则说u可达v. 当然，u可达v时，未必u可达v.有向图G的任意二点都相互可达时，G称为强连通的；若G的任意二点，至少有一点可达另一点，则G称为单侧连通的；若G略去边的方向时是连通图； 则弥G是弱连通的. 强连通图必是单侧连通图； 单侧连通图必是弱连通图. 其逆均不真.
例如图

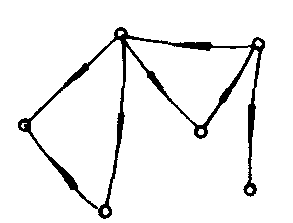
G₁

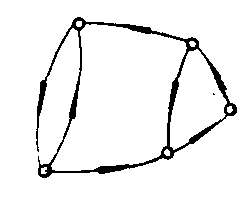
G₂

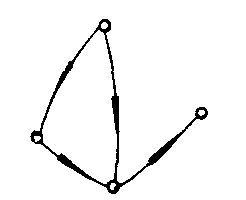
G₃

G₁是弱连通图，G₂是强连通图，而G₃是单侧连通图.