边际替代率biān jì tì dài lǜмаржинльная нóрма(предéльная нóрма)замещéния

边际替代率

在相同的效用或福利水平下，消费者放弃一种商品的数量，和为此必须补偿的另一种商品的数量的比值。如果放弃商品Y的 一定数量(△Y)，增加商品X的一定数量(△X)，则以X代替Y的边际替代率(MRS)可以写作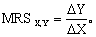希克斯在《价值与资本》(1939年)一书中最先提出这一概念。按照他的解释，边际替代率为负数，且其绝对值呈递减趋势，这是由于物品的消费数量与边际效用成反方向变动。因此，边际替代率又可以用两种物品的边际效用之比来表示：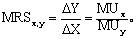

边际替代率Marginal Rate of Substitution

是指在维持消费者满足程度即效用不变的前提下，消费者为增加一单位某商品而愿意放弃的另一种商品的数量。如果消费者只消费两种商品X、Y，那么消费者用X来替代Y的边际替代率MRS_x,y表示为：

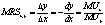
Δy与Δx分别表示x、y两种商品的变动量，-dy/dx是用导数的形式表示边际替代率，在效用函数为连续的情况下，它是更为精确的表达形式。MU_x是X商品对于消费者的边际效用；MU_Y是Y商品对于消费者的边际效用。边际替代率的几何意义是它在无差异曲线某一点的斜率。无差异曲线上各点的边际替代率是不同的。无差异曲线凸向原点的特征表明，边际替代率是递减的。这是由边际效用递减规律所决定的。因为在用X替代y时，随着X的增加，其边际效用MU_x递减，而随着y减少，y的边际效用MU_y递增，因此MU_x/MU_y是递减的。

边际替代率Marginal Rate of Substitution

在维持效用水平不变的前提下，消费者增加一单位某种商品的消费数量时所需要放弃的另一种商品的消费数量。衡量的是从无差异曲线上的一点转移到另一点时，为保持满足程度不变，两种商品之间的替代比例。在无差异曲线上任一点的边际替代率等于该点上无差异曲线的斜率的绝对值。

边际替代率

消费者为保持相同的满足程度，增加某种商品的消费数量与其愿意放弃的另一种商品的消费数量的比率。参见“无差异曲线”。

边际替代率

假定消费者在一定的偏好，技术和资源的条件下，依据一定的价格和一定的收入，对商品的不同组合作出选择。例如有两种商品： 牛肉和布，按照某个消费者的偏好，6个单位的牛肉和2个单位的布，4个单位的牛肉和3个单位的布，2个单位的牛肉和5个单位的布，1个单位的牛肉和8个单位的布等，可以使他得到同等程度的满足。这就是说，两种商品的一系列组合，都可以给这位消费者带来同等程度的满足。同时，这也说明，消费者为了使自己的满足程度不变，当他损失1个单位的牛肉时，就需要一定单位的布来补偿。从例中最后2个组合可以看到，当消费者损失1个单位的牛肉时，需要3个单位的布来补偿，这样才能使他的满足程度不变。这种替代关系，就是边际替代率，换言之，甲商品替代乙商品的边际替代率，就是在消费者满足程度不变的条件下，为增加1单位的甲商品而减少的乙商品的数量。
为了保持消费者满足程度的不变，商品组合中甲商品越减少，则需相应增加的乙商品的数量必然越多。这从我们的生活经验中即可得知： 消费者持有的甲商品越多，而持有的乙商品则越来越少，他对甲商品的评价必然越来越低，而对乙商品的评价则会越来越高。这种边际替代关系，被称为边际替代率递减规律。与无差异曲线上的任何一点相切的直线的斜率，就表示在该点的两种商品的边际替代率。
边际替代率是序数效用论的基本分析工具之一。是由希克斯提出并采用的。它对于解决在经济学中如何表示消费者的偏好，以及将这种偏好尺度构成消费者的福利概念等，具有重要的意义。

边际替代率Marginal Rate of Substitution

消费者在保持相同满足程度的前提下，用一种商品的数量替代另一种商品数量的比率。用无差异曲线的图形来表示，处在同一条无差异曲线上的A点和B点，分别表示两种商品X和Y的不同组合：X₁Y₁和X₂Y₂。因为A和B的总效用是一样的，所以从A点到B点的移动，要求做到减少商品X的消费所失去的效用恰好被增加商品Y的消费所得到的效用(Muy)弥补。用公式表示：

-△Y·MU_y＝△X·MU_x

上式可归纳为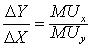

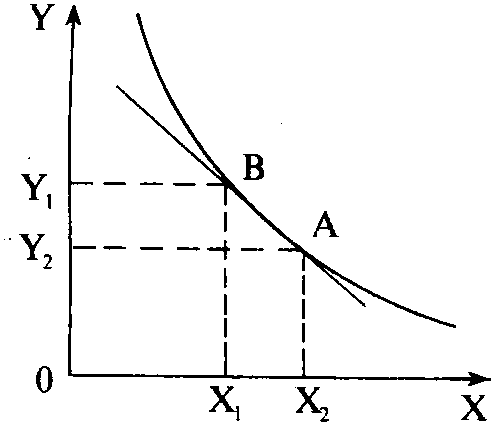
它说明为保持总效用水平不变，边际替代率即一种商品的数量替代另一种商品数量的比率等于两种商品的边际效用之比。

图2

边际替代率Marginal Rate of Substitution

消费者在商品组合中用一种商品替代另一种商品的比率。它表明消费者在保持满足程度或效用水平不变的前提下，为了增加一单位的商品或劳务时所必须放弃的商品或劳务的数量。根据无差异曲线的定义，无差异曲线是表示给消费者带来同等程度的满足水平或效用指数的商品的各种不同组合的曲线。因此一条无差异曲线上的各点，表示的是能够提供同等满足水平的两种商品的不同数量组合 （见图）。图中，I是一条无差异曲线，曲线上各点表示商品X和商品Y不同数量的组合给消费者带来的同等的满足水平。从曲线上任何一点开始，向右下方滑动，意味着Y商品数量减少和X商品的增加，如图中由A点滑动到B点时，Y商品由D数量减少到E数量，X商品由F数量增加到G数量； 反之，曲线上任意一点向左上方滑动时，意味着Y商品数量增加和X商品数量减少。因此，要保持同等的满足水平，无差异选择的两种商品在数量上必然是一增一减的，在两种商品之间就存在一个替代比例问题，以同等满足水平的增加一单位商品或劳务的数量与其必须放弃的另一单位的商品或劳务的数量之比，就形成边际替代率，如图中，A和B的边际替代率为：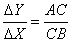

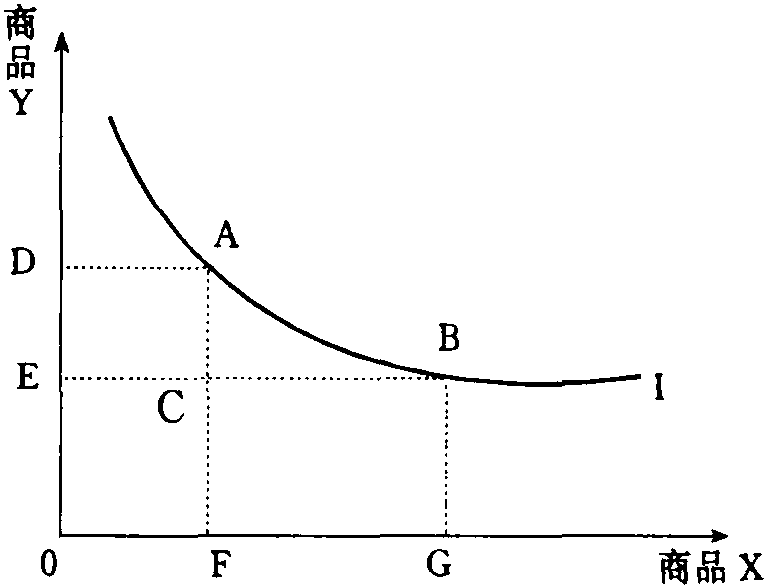
实际上这个边际替代率就是曲线I上的A点和B点之间连接线的斜率，因此，边际替代率的几何意义就是无差异曲线的斜率。无差异曲线凸向原点，斜率递减，这表示边际替代率递减。当A点沿着曲线I由左上方向右下方移动时，商品X越来越多，商品Y越来越少，单位商品X所能代替的商品Y的数量也就越少。这就是序数效用所说的边际替代率递减规律。边际替代率与边际效用在涵义上是相同的。边际效用指一定时间内消费者增加一个单位商品或劳务的消费所得到的增加的效用量。边际替代率表示某一种商品或劳务的增减所引起的另一种商品或劳务的相应增减。假定有X、U两种商品，以MU_X表示商品X的边际效用，以△X表示X的增量，以MU_Y表示商品Y的边际效用，以△Y表示Y的增量，以MRS_XY来表示X替代Y的边际替代率，则：

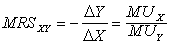
它表示商品X和商品Y的边际效用之比等于它们的边际替代率。序数效用论既然用边际替代率取代边际效用，当然也就用边际替代率递减规律取代边际效用递减规律。

边际替代率Marginal Rate of Substitution

为保持相同的效用水平，消费者增加一种商品的数量与必须放弃的另一种商品的数量之比。通常以MRS_ij或MRS₁₂表示。在效用函数U=U(x₁,x₂，…，x_n)是离散的情况下，其边际替代率其实是平均替代率。若U(x₁,x₂，…，x_n)=U⁰，导出x_j＝f(x₁⁰,x₂⁰，…，x_i，…，x_n⁰,U⁰)，则：

式中x₁⁰,x₂⁰，…，x_n⁰(不含x_i⁰和x_j⁰)和U⁰表示数量不变。如效用函数连续且有一阶、二阶偏导数存在，则：

序数效用论中的边际替代概念与基数效用论中的边际效用概念相对应，它们之间的关系是：

边际替代率是无差异曲线斜率的绝对值。边际替代率可以分为边际私人替代率和边际社会替代率。
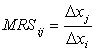
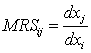
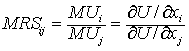
〖参〗序数效用
　边际效用

边际替代率marginal rate of substitution

边际替代率是无差异曲线的斜率，它可以根据无差异曲线的导数求出。由于无差异曲线是以效用为常数的效用函数，即：U(XY)=C，所以它的导数便为：

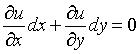
(1)

解无差异曲线的斜率，得

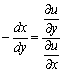
(2)

(2) 式即为x对y的边际替代率。该式表明，在一条无差异曲线的某一点上的x和y的边际替代率，实际上就是y的边际效用和x的边际效用之比。
边际替代率的经济含义是，增加某种商品 (x) 一定数量所造成的效用增加恰好等于减少另一种商品一定数量所造成的效用损失。
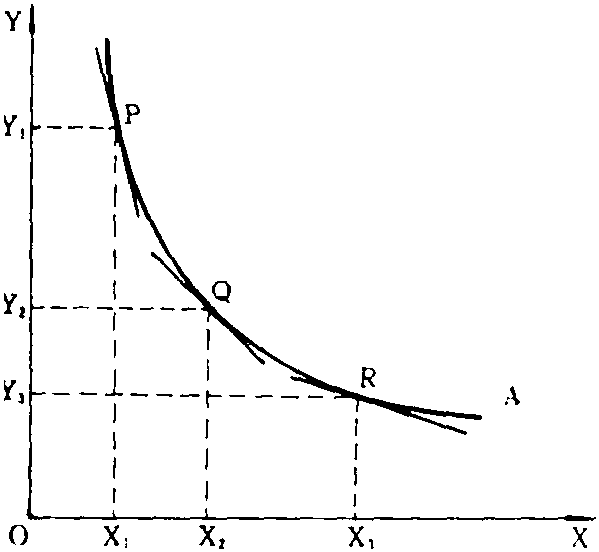
边际替代率呈递减的规律，这就是西方经济学中的“边际替代率递减规律” (the law of decreasing marginal rate of substitution)可以根据下面的无差异曲线图形说明“边际替代率递减规律”。
图中的无差异曲线A上有P、Q、R三点，代表X和Y的三种组合 (X₁Y₁,X₂Y₂,X₃Y₃) 。横轴表示X的数量，且OX₁＝X₁X₂＝X₂X₃。首先从P到Q，若其距离很近或X₁X₂很小，在Q处X对Y的边际替代率则是：

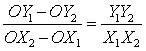
同样，从Q到R,X对Y的边际替代率则是：

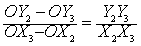
由于X₁X₂＝X₂X₃，并且从图上看，显然Y₁Y₂>Y₂Y₃，所以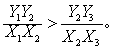这表明从Q到R，边际替代率递减。这是无差异曲线向右下方倾斜的原因。

边际替代率marginal rate of substitution

在保持同等效用水平的条件下，消费者增加一单位某种商品的消费可以代替的另一种商品的消费量。边际替代率是无差异曲线的斜率，用公式表示为：

边际替代率=商品Y的改变量/商品X的改变量

在同等效用水平下，随着一种商品消费数量的连续增加，消费者为得到每一个单位的这种商品所需要放弃的另一种商品的消费数量是递减的，即边际替代率是递减的，这称为边际替代率递减规律。边际替代率递减规律决定了无差异曲线的形状凸向原点。边际替代率递减规律是序数效用论分析消费者行为时的假定。