边际报酬递减规律Diminishing returns law

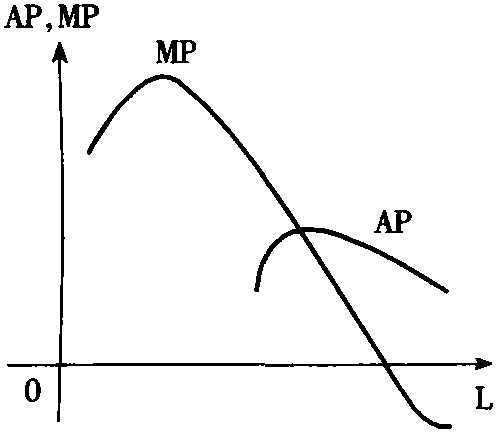
指在技术水平和其他投入物不变的情况下，如果连续增加一种或一种以上的可变物来增加产量，在生产过程达到某一点后，总产量的增加将越来越小，可变投入量与边际产品及平均产量间的关系可用表说明。由此表可以看出，劳动投入为6个单位时总产量最大；在劳动投入为4个单位以前总产量以递增的速度增加，在4个单位以后，总产量以递减速度增加。由图中也可看到其他条件不变时，先是可变要素（此例为劳动）的边际报酬然后是该要素的平均报酬在某点之后递减。最早对报酬递减规律进行明确描述的是法国经济学家杜尔阁。在现代西方微观经济学中，边际收益递减规律是一重要工具，厂商生产要素需求曲线和成本曲线等都是以报酬递减规律为基础的。边际报酬递减规律是一个重要的经济和技术规律，但它并不是普遍适用的。在既定的固定投入没有被充分使用时，增加可变投入后可能出现收益递增。只有在加入相当多同一单位的可变投入后，边际报酬递减规律才生效。边际报酬递减规律是生产要素分为可变投入和固定投入的基础上得出的结论，只适用于可变比例的生产函数。在技术条件不变时，随着可变投入的增加，相对于固定投入而言增加可变投入可使总产量增加，但在一定点之后，新增加的同一数量的可变投入只能和越来越少的固定投入一起发生作用，因而增加相同的可变投入量而带来的产量增量将会越来越少。边际报酬递减规律是分析厂商在各种要素的不同组合下求得最大产量和说明生产可能性曲线概念的理论基础和工具。

资本投入	劳动投入	总产量	平均产量	边际产量
1	1	100	100	100
1	2	240	120	140
1	3	390	130	150
1	4	520	130	130
1	5	6	122	90
1	6	660	110	50
1	7	660	94.3	0
1	8	640	80	-20

边际报酬递减规律Law of Diminishing Marginal Returns

见“边际收益递减规律”。

边际报酬递减规律

见“边际收益递减规律”。