辛卜森公式xinpusen gongshi

如图1，一个几何体夹在两个平行平面之间，若用平行于底，且与下底的距离为x的平面去截这一几何体，截面面积A是x的不超过三次的多项式函数，即A=a₀x³+a1x2+a₂x+a₃(a_0a1,a2,a3∈R)，则该几何体的体积是

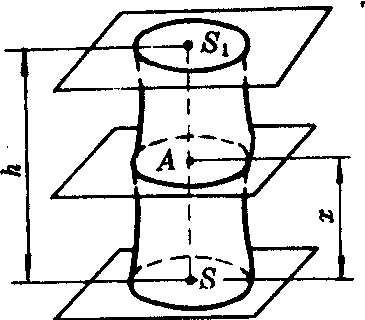
图1

其中h是几何体的高；S₁和S分别是几何体的上、下底面积；S0为中截面面积.
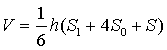
上面的公式叫辛卜森公式.

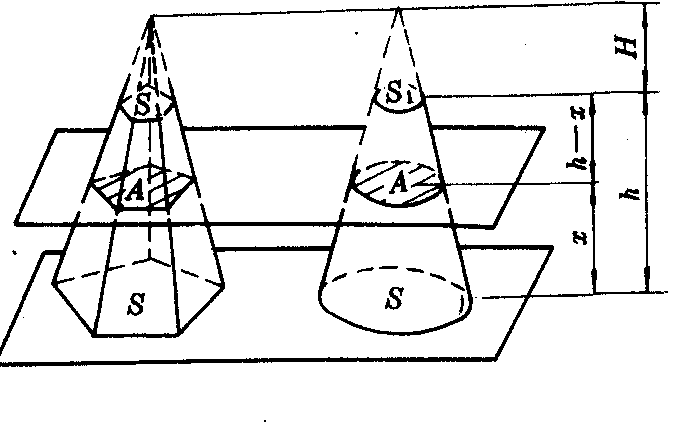
图2

下面说明柱、锥、台、球、球缺等可以用辛卜森公式求体积.
❶柱、锥、台的体积 如图2，用S₁,S和A分别表示台体（棱台或圆台）的上、下底面和平行于底面任意截面面积，则有

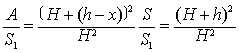
由二式消H, 得

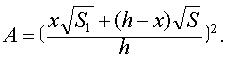
上式表明A是x的二次函数，所以台体体积可以用辛卜森公式计算.

因为台体的中截面

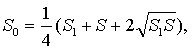
把

它代入辛卜森公式，可得到通常应用的台体体积公式

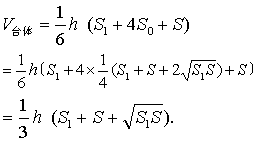
当台体的两底全等时，就变成了柱体（棱柱或圆柱），这时S₁＝S=S0，将它们代入辛卜森公式，得

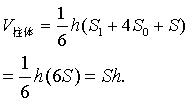
这就是通常应用的柱体体积公式.
当台体的上底面退缩成一点时，它就变成了锥体

（棱锥或圆锥），这时

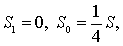
将它们代入辛

卜森公式， 得

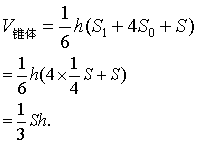
这就是通常应用的锥体体积公式.

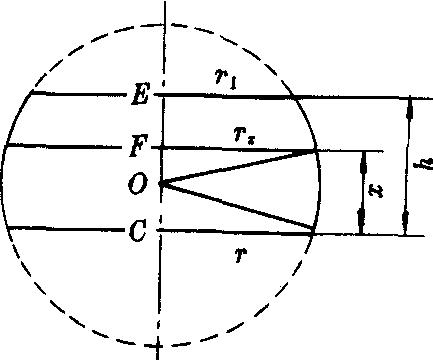
图3

❷球台、球和球缺的体积 如图3，用r1,r和rx分别表示球台的上、下底面半径以及平行于底面且距下底面为x的截面圆半径，设OC=d，则OE=h-d,OF=x-d.

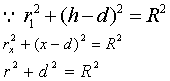
从前两式减去后式， 得

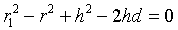
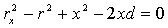
消去d, 得

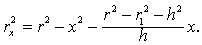
所以截面面积

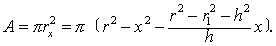
上式表明，A是x的二次函数，因此球台的体积可以用辛卜森公式计算.
因为S₁＝πr1²,S=πr².设r₀是中截面圆半径，当x=h/2时，则

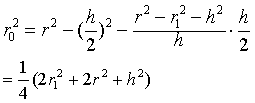
所以中截面面积为

将这些值代入辛卜森公式，得到通常使用的球台的体积公式

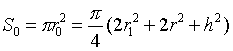
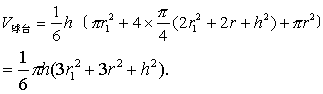
当r₁＝0,r=0时，球台变成球体，这时h =2R,S1=S=0,S₀＝πR².把这些值代入辛卜森公式，可得到通常使用的球体体积公式

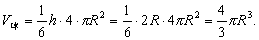
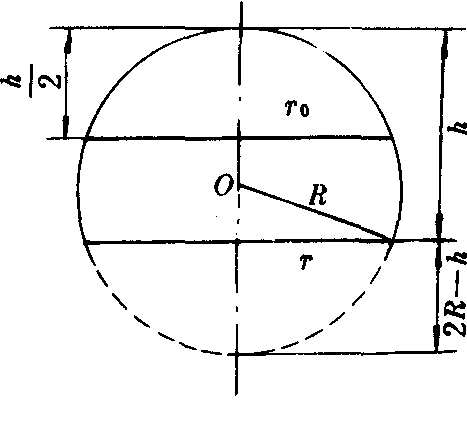
图4

当r₁＝0，即S₁＝0时，球台变成球缺.

由图4可知

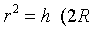
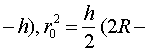
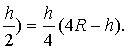
所

以

S=πh(2R-h),S0

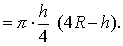
把这些值代入辛卜森公式，可得到通常使用的球缺体积公式

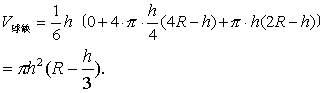
至此，可以说辛卜森公式是中学立体几何课本里所介绍的柱、锥、台、球、球缺等几何体的体积公式的总公式，因而人们把它称为万能求积公式.