贾宪

北宋数学家。约十一世纪时人。曾撰《黄帝九章细草》和《算法敩古集》，都已失传。杨辉《详解九章算法》(1261年)曾引他的《开方作法本源》（指数为正整数的二项定理的系数表）和增乘开方法（求高次幂的正根法）。“开方作法本源”的出现比帕斯卡三角形早六百年。增乘开方法的计算程序大致和霍纳(1786—1837年)的方法(1819年)相同，而比它早七百七十年。

146 贾宪

北宋数学家。约生活于11世纪上半叶。生平事迹无法详考。曾从师于北宋著名天文学家、数学家楚衍。做过左班殿直。“运算亦妙，有书传于世”(王洙：《王氏谈录》)。 撰《黄帝九章算法细草》9卷、《算法斅古集》2卷及《释锁》，均已失传。南宋数学家杨辉在其著作中引用了《黄帝九章算法细草》的部分内容，使贾宪的两项重要成就：贾宪三角、增乘开方法得以保存并流传至今。这是数学史上两项重要成就，它导致求高次方程实根的一整套方法。对于其后宋元数学的高度发展有着重要的奠基和肇始之功。

贾宪约1050Jia Xian

北宋数学家，著 《算法斅古集》和 《黄帝九章算法细草》，均已失传，后者的一部分内容被南宋数学家杨辉采入 《详解九章算法》(1261). 据杨辉引述，贾宪创造了增乘开方法. 即求解Xⁿ＝A的算法程序，基本思想与19世纪意大利鲁斐尼、英国霍纳所得结果一致.他的“开方作法本源”即(x+a)ⁿ展开式的系数表及其构造方法，远远早于阿拉伯阿尔·卡西、德国阿披亚纳斯、法国帕斯卡的工作，西方称之为帕斯卡三角，实际上应称为贾宪三角.

贾宪11世纪Jiaxian

中国数学家。北宋著名数学家楚衍的学生，曾任下级军官，1050年前后已经因善算知名于世。数学著作有《算法教古集》二卷，《黄帝九章算法细草》九卷，均已失传，后一书的部分内容被南宋杨辉采入《详解九章算法》(1261)，保存了两项杰出的成就， 增乘开方法与开方作法本源。
增乘开方法是通过随乘随加开高次方的一种方法，其原理相当于连续地使用综合除法。从解方程的角度看，它是解二项方程xⁿ-A=0的演算程序，基本思想与19世纪意大利鲁斐尼(Ruffini, P.,1804)、英国霍纳 (Horner. W. G., 1819) 所得结果一致。
开方作法本源，即二项式系数表，贾宪明确地给出了这张表及其构造方法。由它的名称和杨辉的引述看，最初它是用来开高次方和解高次方程的， 但即使在宋元时代，人们对它的认识也远远超过了这个范围，朱世杰就曾利用它导出垛积术中一些重要结果， 与贾宪大致同时，印度人也得到了这张表，并称之为 “金字塔图”， 其他国家则要晚得多。阿拉伯数学家卡西(al-Kashi⁾ 在1127年基本上重复了贾宪的工作。从1527年

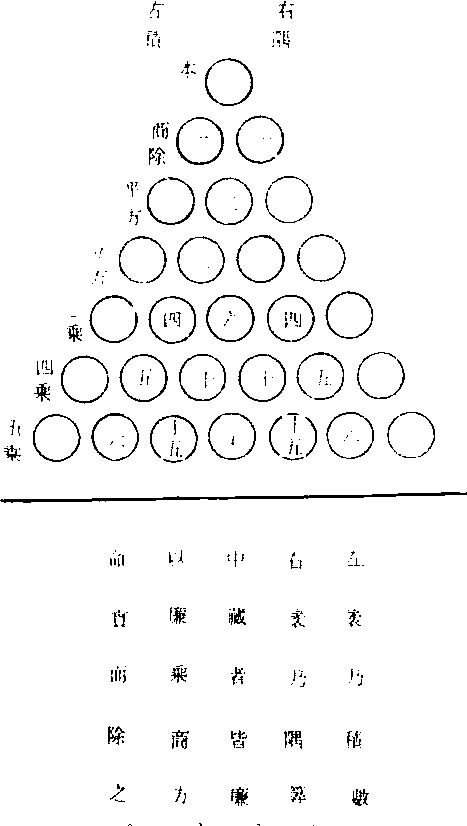
开方作法本源
德国数学家阿皮亚纳 斯 (Apianus.P.) 的 《实用算术》起这张表才出现在欧洲数学家的著作中， 在16世纪它已被许多数学家所使用。欧洲人习惯于称它为帕斯卡三角形， 但法国数学家帕斯卡直到1654年才进行有关的研究， 公允的名称应该是贾宪三角
形。

贾宪约11世纪

中国北宋数学家。据记载其“开方作法本源”图（指数为正整数的二项定理的系数表）和增乘开方法（求高次幂的正根法），比西方的方法早六七百年。著《黄帝九章细草》等，均失传。

贾宪

北宋数学家。曾撰《黄帝九章算法细草》 和 《算法斅古集》，都已失传。杨辉《详解九章算法》曾引他的《开方作法本源》 （指数为正整数的二项定理的系数表）和“增乘开方法” （高次幂的求正根法）。《开方作法本源》的出现比巴斯卡 (B. Paseal) 三角形早600年。增乘开方的计算程序大致和霍纳(W. G. Horner) 方法 (公元1819年) 相同，而比它早770年。