误差分析方法wuchafenxi fangfa
运用物理实验误差理论分析物理实验中各类问题的一种方法。通常指对一个实验误差的计算和综合分析。它可为解决物理实验中的具体问题,提高实验教学的质量提供一定的逻辑依据。对一个具体实验进行误差分析,可包括下列内容:
❶根据实验原理、装置、合理选配实验仪器,使实验误差不会因个别仪器的误差而显著增大,也避免造成盲目追求使用高、精、尖的仪器设备。选配的依据是使实验中各仪器引起测量的最大相对误差在同一数量级。
❷比较误差传递公式中的系数,看是否可以对某量进行单次测量。
❸实验后计算实验的绝对误差或相对误差。
❹据误差的计算结果分析误差的主要来源,提出改善测量精确度的方法,其中要特别注意寻找在原有仪器设备条件下提高精确度的具体可行方法。
例如,试在测量直径D为0.8厘米,高h为3.2厘米的圆柱体积之前进行误差分析。
❶对偶然误差,圆柱体积为v=πD2h/4,据N=xkym/zn的标准误差传递公式,当k=2,m=1,n=0时,有σv/V=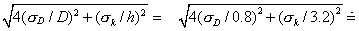
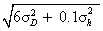 可知σD与σA的系数比较约为
可知σD与σA的系数比较约为 倍。
倍。
❷对仪器的误差,据仪器误差传递公式有,△V/V=2△D/D+△h/h=2△D/0.8+△h/3.2=2.5△D+0.3△h,可知△D与△h的系数比约为8。据❶
❷计算可得如下结论。其一,本实验中误差的主要来源为直径的测量。其二,提高测量D的仪器精度,增加测量D的次数会有效减少V的测量误差。其三,测h的仪器精度可以比测D的仪器大一个数量级而基本不影响仪器的匹配。其四,D不宜单次测量,而h可考虑单次测量。
又如,测量铜块的比热。若采用感量为10毫克,称量为200克的9级天平和最小刻度0.2℃的温度计,测得量热器质量为m1=(27.050±0.005)克,水的质量m2=(195.950±0.005)克,铜块质量m3=(361.200±0.005)克,水和量热器的初温t1=(21.2±0.01)℃,铜的温度t2=(100.0±0.1)℃,放铜后的混合温度t=(32.6±0.1)℃。试对该实验进行误差分析,(已知量热器比热c1=0.214卡/克℃)。据热平衡方程(m1c1+m2c2)(t-t1)=m3c3(t2-t),铜的比热c3=(m1c1+m2c2)(t-t1)/m3(t2-t)=9.04×10-2卡/克℃,据N=xkym/zn的仪器误差传递公式,令x=m1c1+m2c2,y=t-t1,z=m3(t2-t),k=m=n= 1,有c3的相对误差△c3/c3=|△(m1c1+m2c2)|/(m1c1+m2c2)+|△m3|/m3+|△(t-t1)|/(t-t1)+|△(t2-t)|/(t2-t),再据N=x±y的仪器误差传递公式,上式可化为(c1△m1+c2△m2)/(m1c1+m2c2)+△m3/m3+(△t+△t1)/(t-t1)+(△t2+△t)/(t2-t)=0.00003+0.00002+0.02+0.003=2.3%。可知,误差主要由温度测量引起,误差主要来源为(△t+△t1)/(t-t1)一项,其次为(△t2+△t)/(t2-t)。在不改变温度计的情况下,只能增大分母(t-t1)与(t2-t)。为此,据热平衡方程求出t=(m1c1t1+m2c2t2)+m3c3t3)/(m1c1+m2c2+m3c3),变形为
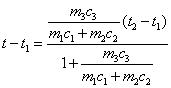
- 辟雍博士是什么意思
- 辟雍司业是什么意思
- 辟雍大司成是什么意思
- 辟雍录是什么意思
- 辟雍明堂镜室是什么意思
- 辟雍正是什么意思
- 辟雍直学是什么意思
- 辟雍砚是什么意思
- 辟雍硯是什么意思
- 辟雍碑是什么意思
- 辟雍纪事是什么意思
- 辟雍讲义是什么意思
- 辟雞是什么意思
- 辟非是什么意思
- 辟非老人是什么意思
- 辟非黄符是什么意思
- 辟面是什么意思
- 辟韩是什么意思
- 辟领是什么意思
- 辟鬼除邪方是什么意思
- 辟鸡是什么意思
- 辟鸱是什么意思
- 辟鼠是什么意思
- 辟:是什么意思
- 辠是什么意思
- 辠尤是什么意思
- 辠戾是什么意思
- 辠过是什么意思
- 辡是什么意思
- 辡部是什么意思
- 辢是什么意思
- 辣是什么意思
- 辣丁中华合璧字典是什么意思
- 辣不唧儿是什么意思
- 辣不辣来甜不甜是什么意思
- 辣丝丝是什么意思
- 辣乎乎是什么意思
- 辣乎儿的是什么意思
- 辣乎儿辣乎儿是什么意思
- 辣人是什么意思
- 辣作是什么意思
- 辣侉是什么意思
- 辣侯侯的是什么意思
- 辣兴兴是什么意思
- 辣农是什么意思
- 辣凑是什么意思
- 辣列是什么意思
- 辣利是什么意思
- 辣利婆是什么意思
- 辣刮是什么意思
- 辣势能是什么意思
- 辣勒是什么意思
- 辣卜是什么意思
- 辣厉婆是什么意思
- 辣发是什么意思
- 辣吼吼格是什么意思
- 辣呆是什么意思
- 辣呲忽咧是什么意思
- 辣味是什么意思
- 辣味与凉水是什么意思