共线性的诊断与评价

---

文献中对共线性一直没有严格的定义。

术语Collinearity、multicollinearity、ill conditioning都用来表示共线性。从字面上，两个变量共线性是指两个变量的数据向量落在一条直线上，即在一维子空间上。

一般来说，k个变量共线性，是指如果这k个变量的数据向量落在维数小于k的子空间上，即其中一个向量可以用其它几个向量线性表示。

实际上，这种精确的共线性是很少出现的，共线性只是近似意义上的。

在线性回归模型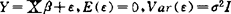中，共线性是指设计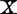矩阵中列向量与列向量之间是否存在共线性。所以从本质上说回归模型中的共线性是设计矩阵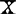的数据特征，而不是回归模型的统计特征。

但在线性回归的许多应用领域中，数据常常是非试验数据，这时数据之间常常出现共线性，那么对于建立在该数据基础上的线性回归模型的统计方面是否会出现问题?答案是肯定的。共线性虽不是统计问题，但对二乘估计及其它估计有很重要的影响。

共线性的诊断与评价就是要对数据矩阵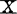中共线性的存在提出诊断方法，研究共线性存在时，对回归估计等的影响程度进行评价，并提出相应治疗措施。

关于对数据矩阵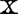中共线性的诊断，人们提出了一些方法，最直接的就是直观诊断法。

直观上，实际工作者认为变量之间应呈现某种规律，如回归系数的符号；另外有些变量实际工作者对其重要程度有一个认识。如果回归结果跟想象的不符，则人们常认为数据矩阵中有共线性存在，或用共线性来解释这种不符合。

但这种不符合的出现并不是共线性的充分必要条件。下面介绍几种诊断方法：

相关阵R的检验法。

当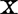是中心标准化时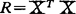，，当某两个变量之间的相关系数很大时，确实表明这两个变量之间存在共线性。

但可能有3个或更多个变量之间存在共线性，而没有两个变量之间存在高相关，此时，用R就不能诊断出来。另外相关阵R不能揭示在变量之间存在几个近似共线性关系。

方差膨胀因子诊断法。

当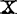是中心标准化长度为1的数据矩阵时有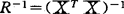，R^－1的对角元r_ii称为方差膨胀因子VIF_i［chatterjee和Price(1977)］。它与X_i的多重相关系数R_i的关系是。

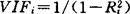式中VIF_i称为方差膨胀因子是因为第i个回归系数的方差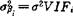，可见VIF_i很高，意味著R_i→1，即出现共线性，引起第i个回归系数的方差变大。

但这里出现与用R诊断同样的问题。

另外对VIF_i的高低无法给出一个有意义的界限。

Farrar与Glauber(1967)技术。

设Z是来自p维正态分布的n个样本，且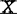是中心标准化的，则R=Z^TZ。当Z的列完全共线性时，det R=0，当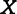的列正交时，det R=1′。从而可用detR去检验Z中的列偏离正交或共线性的程度。

Farrar和Glauber提出用统计量x²=－(n－1－(2p+5)／6)lndet R，这里x²～x²(p(p－1)／2)，去检验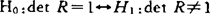。如显著，认为有共线性。进一步，他们还提出用偏相关系数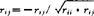去判定共线性的类型。该方法同样存在许多问题。

特征法诊断。目前普遍采用矩阵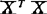或相关阵R的特征根诊断共线性的存在。Kendall(1975)和Silevy(1969)建议如果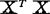有很小的特征根存在，说明共线性存在。但对“小”，没有明确的界限。

条件数诊断。

在数值分析中，广泛采用条件数作为诊断量测。方阵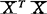的条件数定义为k=λ₁／λ_p，其中λ₁≥λ₂≥……≥λ_p＞0为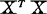的特征根。一般认为k≥100存在较强共线性，k＞1000存在严重共线性。但条件数不能告诉我们有几个共线性关系以及每个共线性关系中包含哪几个变量。

回归系数方差分解比联合条件指标诊断法。这是目前发展得比较好的一种方法。该方法由Belsley等在1980年提出的。设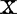的列标准化。

如模型有常数项，则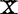包含1。

对任意矩阵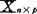可分解成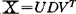，其中U_n×p，V_p×p，D_p×p，且U^TU=V^TV=1，D=diag(μ₁，μ₂，…，μ_p)，μ_i≥0，i=1，2，…，p，μ_i称为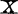的奇异值。

则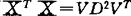，V是对角化Z^TZ的特征向量。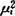是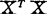的特征根，i=1，2，…，p。

从计算角度，矩阵Z的奇异值分解的算法要比算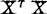的特征系统数值稳定性好，尤其在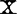是病态时更是如此，人们发现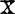，列中的近似线性关系对应著有较小的奇异值。依据条件数的定义，k(x)=μ_max／μ_min≥1，其中μ_max，μ_min为Z的非零最大和最小奇异值，它反映病态条件的程度。于是定义η_k=μ_max／μ_k，k=1，2，…，p，为矩阵Z的第k个条件指标。

如果出现高条件指标，就认为Z列中有近似线性依赖。

大量的模拟研究表明，如果共线性很弱，条件指标小于10，共线性很强，条件指标在10到30之间，共线性很严重，条件指标在30以上乃至100以上。由此有n个高条件指标，就有n个共线性关系。

进一步，通过回归系数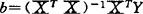的方差Var(b)

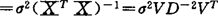，进行分解有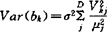可见Var(b_k)分解成p项和，每项只与唯一的一个奇异值对应。令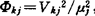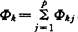，，则定义第k、第j个方差分解比为π_jk=Φ_kjΦ_k，k，j=1，2，…，p，从而存在n个条件指标诊断为高条件指标，就有n个共线性关系。

在与高条件指标相应的方差分解比中，有n个回归系数的方差分解比大(超过0．5)，就认为有n个变量包含在共线性关系中，并且这些方差分解比的大小提供了对应的回归估计受共线性影响的程度。

诊断出线性回归模型中共线性存在以后，必须消除或设法减弱共线性，以便提高最小二乘估计的精度，提高预测的准确性。这种补救的方法一是引进新数据，但此时新数据可能成为强影响点；另一种是利用Bayes技术，通过对回归系数β引进一些随机约束来改进估计；还有一种是用有偏估计如岭估计方法，通过引进岭参数，增强二乘估计，主成分估计等的稳定性。

。

【参考文献】：

1 Chatterjee S,et al. Regression Analysis by Example. New York :John Wiley and Sons

2 Kendall M G. A course in Multivariate Analysis. Griffin, London

3 Farrar D E, et al. Review of Econmics and statistics, 1967, 49:92～107

4 Silevy S D. J Roy Satist. Soc, Ser B,1969,31:539～552

5 Golub G H, et al. Numerische Mathematik, 1970,14:403 ～420

6 Kumar T K. The Problem of Multicollinearity:A survey, Abt Associates, Inc, Cambridge, Mass,1975

7 Belsley DA, et al, Regression Diagnostics, New York;John Wileyand Sons,1980,85～261

8 戴伯新．数学的实践与认识，1989，453～61

(南京理工大学戴伯新撰；项可风审)

上一篇：概率度量空间上的非线性分析
下一篇：向量值最优化问题的对偶性

"共相共相

---

共相问题是中世纪哲学讨论最多的问题之一。

英语中的“共相”(universals)一词源自拉丁文uneversalis，原意是“属于一切的东西”。古希腊哲学家已经开始讨论共相问题，但他们使用的术语不同。

与“共相”一词相关的概念有“种”、“属”、“类”，与它相对的概念是“殊相”(Partieulars)、“个体”(individuals)。具体地说，共相问题就是共相的本体论地位问题，其相是不是实在的?如果是，那么它们存在于什么地方?一般认为，把共相问题引入中世纪的是波埃修斯。

他把波尔菲利的《亚里士多德〈范畴篇〉导论》(Isagoge)译成了拉丁文，从而也把共相是否实在的问题引入了中世纪。中世纪哲学家们在共相问题上形成了三大派观点。

概括地讲，唯实论(Realism)认为共相是一种独立存在于精神之外的实在；概念论(Conceptualism)认为共相仅仅在心灵中具有实在性；唯名论(Nominalism)则主张共相不过是名称，在心灵中和心灵外都没有实在性。这种区分只是大致的区分，各派观点内部也有很多分歧，例如，唯实论就分为极端唯实论和温和唯实论。另外，由于中世纪的哲学与神学具有不可分离的密切关系，所以，关于共相问题的讨论也具有重要的神学意义。

例如，极端唯名论者洛色林就曾被指控为主张三神论。

奥古斯丁像柏拉图一样在共相问题上是个极端的唯实论者，他认为共相是实在的，是上帝的观念，创造世界的范型(archetype)。他的观点对中世纪的弗兰西斯派哲学家有巨大影响。

波埃修斯坚持亚里士多德的温和唯实论，承认共相是实在的，但认为它们不独立存在，而是作为形式存在于事物中。爱里根纳主张绝对的唯实论。阿维森纳坚持亚里士多德的观点，同时认为，人的精神作用仅仅给予共相以潜在的存在。

要现实地把握共相，人必须与能动理智产生联系，能动理智是上帝与人之间的中介。

安瑟尔谟主张唯实论，认为抽象的心智对象不仅存在于可感觉的事物中，还存在于上帝的心中。他对洛色林的观点提出了批判。

洛色林被认为是唯名论的创始人。据安瑟尔谟和阿伯拉尔的记述，洛色林认为共相仅仅是“发出的声音”(flatus vocis)或“仅仅是语词”。

香浦的威廉是洛色林的学生，他主张绝对唯实论。威廉认为，同一个本质属性同时存在于一个属的所有元素中。他后来改为主张一个属的个别元素不是本质地相同，而是“无差别地”相同。

阿伯拉尔先后就学于洛色林和香浦的威廉，他力图找到一条中间的道路。

他的观点被叫做概念论，但也有人认为他是个温和的实在论者。阿伯拉尔认为，共相存在于心灵中，也存在于事物中，但不是像人们想的那样存在于事物中。

托马斯·阿奎那一方面接受了阿伯拉尔和索尔兹伯里的约翰(John of Salisbury)的温和实在论观点，同时也坚持了奥古斯丁的某些观点。

他认为，我们可以以三种方式谈论共相：1．事物之前的共相(universals ante rem)存在于上帝的心灵中；2．事物之中的共相(universals in rem)是个别事物的具体的个别本质；3．事物之后的共相(universals post rem)是心灵中的抽象的一般概念。

邓斯·司各脱把他关于形式区别的观点应用于关于共相的讨论，认为某一个人的“唯此性”(haecceitas)或个别本质与一般的人性只有形式区别，所以，共相是以事物为根据的，但不存在于事物中。

奥康的威廉被认为是唯名论者。

他认为，共相只是一般名称。威廉批判了各种形式的唯实论观点，认为不存在与一般名称相对应的一般事物。

实际存在的只有个别，任何可断定为属于许多事物的东西本质上都只存在于心灵中。

上帝心中并没有创世的范型(exemplars)，所以，事物之间的相似性完全是人的观察的结果。约翰·梅杰领导了奥康的唯名论在15世纪后半叶和16世纪前半叶的苏格兰的复活。