薛定谔方程xuedinge fangcheng

描述原子核外电子运动状态的方程，是量子力学中研究微观粒子的基本方程。1926年E.薛定谔根据核外电子波粒二象性，考虑到原子中电子是处于定态，而且是量子化的。在波动学中只有驻波是量子化的，将定态与驻波类比，得出了这个方程，故称做薛定谔方程。
一维驻波的方程为：

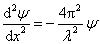
而原子核外的电子可以在X、y和z三个方向上运动，因而上式可变成：

(式中h是普朗克常数，m近似是电子质量，而v是电子的速度)。因而：

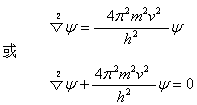
不过体系的总能量E是由动能K加势能U组成的

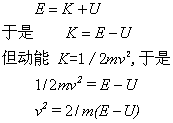
将v²代入上述方程式，就得到人们熟知的薛定谔方程式或称薛定谔第一方程式：

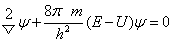
薛定谔方程是用来描述质量为m的微观粒子，在势能为U的势场中运动，其运动状态和能量关系的定态方程。薛定谔方程的每一个合理的解ψ，都表示该粒子运动的一个稳定状态，与这个解相应的常数E，就是粒子处于这个稳定状态的能量。尽管薛定谔方程式不是严格推导出来，而是由其基本假设类比得出的，但半个多世纪以来，大量的实验事实已证明了它的正确性。它是处理原子、分子中电子运动状态的基本方程。1928年P.A.M.狄拉克运用相对论原理，将时间t引入薛定谔方程式中，使其更加完善，这也称薛定谔第二方程式。

---

薛定谔方程xuedinge fangcheng

描述微观粒子运动状态的波函数Ψ(x,y,z,t)所遵循的方程。也称作波动方程。是奥地利物理学家薛定谔(E.Schrodinger,1837～1961年)于1926年提出的。薛定谔方程是量子力学中的基本方程；它在量子力学中的地位与牛顿方程在经典力学中的地位相当。在给定条件下若已知微观粒子在某一时刻的状态，可由薛定谔方程求出它在以后任一时刻的状态。其一般形式为：

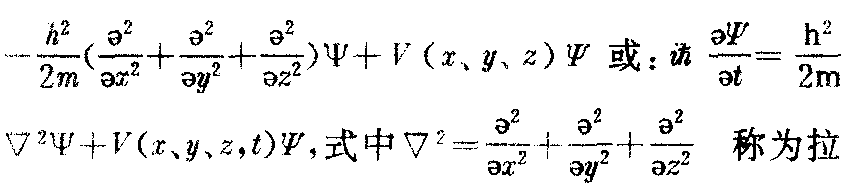
普拉斯算符，i=是虚数，m为粒子的静止质量，V(x、y、z、t)是粒子在外场中的势能，称为势函数。粒子所处的环境（力场）不同，就有不同的势函数。解薛定谔方程，得出描述微观粒子运动状态的波函数，就可由波函数的模的平方得出粒子在不同时刻、不同位置处出现的概率密度。因为在解方程时需要根据给定的初值条件和边值条件，还需考虑波函数必须满足的标准条件，所以只有当一些物理量具有某些特定数值时，方程才有解，从而得到量子化的结果。这些特定的数值叫做该物理量的本征值，相应的波函数叫做本征函数或本征解。
当势能函数与时间无关，仅为坐标的函数时，波函数可以写成：

这种波函数所描述的状态称为定态。Ψ(x、y、z)所满足的方程为：

这个方程称作定态薛定谔方程。其解Ψ(x、y、z)称为振幅波函数，简称波函数。其模的平方就是定态时粒子的概率密度。E为定态时微观粒子的能量。可见微观粒子处于定态中时有确定的、不随时间改变的能量和概率密度。
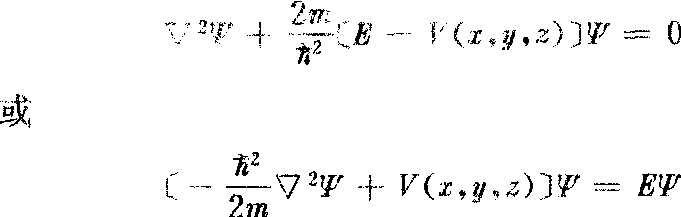
薛定谔方程无法由某种理论或数学方法推导或证明，实际上它是一个假设或定律，其正确性是靠它对一些问题所做的理论计算与实验结果相符合来验证的。从它建立以来关于低能微观粒子的大量实验事实都表明，用薛定谔方程进行计算所得到的结果与实验结果相符合，因此，以薛定谔方程为基本方程的量子力学，被认为是能够正确描述微观系统状态的近代物理理论。薛定谔方程只适用于低速的、非相对论情况。在相对论情况下，需要用狄拉克方程或克莱因—高登方程。

薛定谔方程

Schr⍥dinger equation