全集:如果集合S含有我们所研究的各个集合的全部元素,这个集合就可以看作一个全集,全集通常用U表示.
显然,一切集合都是这个全集的子集.
补集:一般地,设U是一个集合,A是U的一个子集(即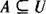 ),由U中所有不属于A的元素组成的集合,叫做子集A在全集U中的补集(或余集),记为
),由U中所有不属于A的元素组成的集合,叫做子集A在全集U中的补集(或余集),记为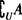 ,即
,即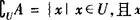
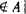
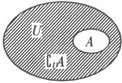
如图: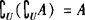 ,
,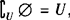 ,
,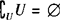 ,
,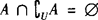 ,
,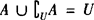 .
.
例1 已知集合A={x|x2—3x+2=0},B={x|x2—ax+3a—5=0},若A∩B=B,求实数a的值.
解 A=}x|x2—3x+2=0}
={x|(x—1)(x—2)=0}={1,2},
由x2—ax+3a—5=0知△=a2—4(3a5)=(a—2)(a—10).
∵A∩B=B,∴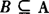 .
.
∴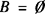 或B={1}或B={2}或B={1,2}.
或B={1}或B={2}或B={1,2}.
若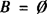 ,则△<0.此时2
,则△<0.此时2
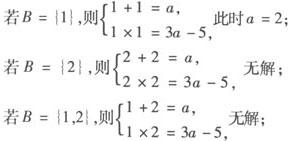
综上,a的范围为[2,10),即当2≤a<10时,均有A∩B=B.
例2 分别标出下图中❶ ❷ ❸ ❹ 所代表的区域.
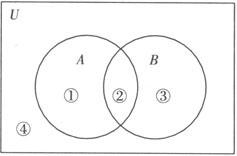
解 ❶ 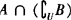 .
.
❷ A∩B.
❸ 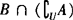 .
.
❹ 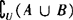 或
或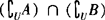 .
.
- r2013010010000174是什么意思
- r2013010010000175是什么意思
- r2013010010000176是什么意思
- r2013010010000177是什么意思
- r2013010010000178是什么意思
- r2013010010000179是什么意思
- r2013010010000180是什么意思
- r2013010010000181是什么意思
- r2013010010000182是什么意思
- r2013010010000183是什么意思
- r2013010010000185是什么意思
- r2013010010000186是什么意思
- r2013010010000187是什么意思
- r2013010010000189是什么意思
- r2013010010000190是什么意思
- r2013010010000191是什么意思
- r2013010010000192是什么意思
- r2013010010000193是什么意思
- r2013010010000194是什么意思
- r2013010010000195是什么意思
- r2013010010000196是什么意思
- r2013010010000197是什么意思
- r2013010010000198是什么意思
- r2013010010000199是什么意思
- r2013010010000200是什么意思
- r2013010010000201是什么意思
- r2013010010000202是什么意思
- r2013010010000203是什么意思
- r2013010010000204是什么意思
- r2013010010000205是什么意思
- r2013010010000206是什么意思
- r2013010010000208是什么意思
- r2013010010000209是什么意思
- r2013010010000210是什么意思
- r2013010010000211是什么意思
- r2013010010000212是什么意思
- r2013010010000213是什么意思
- r2013010010000214是什么意思
- r2013010010000215是什么意思
- r2013010010000216是什么意思
- r2013010010000217是什么意思
- r2013010010000218是什么意思
- r2013010010000219是什么意思
- r2013010010000220是什么意思
- r2013010010000221是什么意思
- r2013010010000222是什么意思
- r2013010010000223是什么意思
- r2013010010000224是什么意思
- r2013010010000225是什么意思
- r2013010010000226是什么意思
- r2013010010000227是什么意思
- r2013010010000228是什么意思
- r2013010010000229是什么意思
- r2013010010000230是什么意思
- r2013010010000231是什么意思
- r2013010010000232是什么意思
- r2013010010000233是什么意思
- r2013010010000235是什么意思
- r2013010010000236是什么意思
- r2013010010000237是什么意思