自回归综合移动平均数预测ARIMA forecast

是指一种时间序列分析法，它是在1970年由博克斯(G.E.P.Box)和詹金斯(G.M.Jenkins)建立的。两位学者定义了自回归综合移动平均及季度自回归综合移动平均两类模型，并且提供了从这两类模型中选择一个合适模型的方法。(1) ARIMA模型的理论架构。假定{Y_t}(t=0,±1,±2，…)是由随机过程产生的等时距系列，具备稳态与可逆转的特性。再设{a_t}(t=0,±1,±2，…)代表“白噪音”（即误差项）。并假定a_t^iid～N(o,δ_a²⁾。iid表示独立且同分布。可用两种完全不同的模型来表现Yt数列的产生过程。
❶自回归模型(简写为AR(P))，即将时序的现在值Y_t对其过去值Y_t-1,Y_t-2，…，Y_t-p，进行回归，由此得到如下AR(P)模型(即P阶自回归模型)

y_t＝₁y_t-1+₂y_t-2+…+_py_t-p+a_t

或变为(1-₁B-₂B²-…-_pB^p)y_t＝a_t其中y_t＝Y_t-μ,μ为均值，₁₂，…，_p为自回归系数，B为滞后移动运算子，P为滞后次数。
❷移动平均模型(简写为MA(q))，即把时序的现在值Y_t表示为现在和过去冲击（误差）的移动平均。MA(q)模型的数学表示为：

y_t＝a_t-θ₁a_t-1-θ₂a_t-2-…-θ_qa_t-q

或写为y_t＝(1-θ₁B-θ₂B²-…-θ_qB^q)a_t 其中，θ₁,θ₂，…，θ_q为移动平均系数，q为移动次数。上式为q阶移动平均模型。有限次数的AR(P)模型可以改写为无限次数的MA(∞)模型，即
y_t＝φ_p^-1(B)a_t 其中φ_p(B)=1-₁B-₂B²-…-_pB^p。
以AR(1)为例：

y_t＝(1-₁B)^-1a_t|₁|<1
　=(1+₁B+₁²B²+…)a_t

同样，有限次数的MA(q)模型亦可改写为无限次数的AR(∞)模型。如此，Y_t数列的产生可以完全以AR模型或完全以MA模型来表现。但实际上，为达到模型的“精简”，常常有必要同时考虑AR与MA两部分，而以ARMA(p,q)的混合模型来表示Y_t数列。即：

y_t＝₁y_t-1+₂y_t-2+…+_py_t-p+a_t-θ₁a_t-1-θ₂a_t-2-…-θ_qa_t-q

或写为：

(1-₁B-₂B²-…-_pB^p)y_t＝(1-θ₁B-θ₂B²-…-θ_qB^q)a_t

如ARMA(1,1)可写为

(1-₁B)y_t＝(1-θ₁B)a_t

为进一步考虑非稳态数列，可将上述ARMA(p,q)模型一般化。即对序列Y_t取d次差分，再做ARMA计算，这就是最一般的ARIMA(p,d,q)模型：
φ_p(B)(1-B)^dy_t＝θ₀θ_q(B)a_t 其中，_p(B)=1-₁B-₂B²-…-p_pB^p,θ_q(B)=1-θ₁B-θ₂B²-…-θ_qB^q,θ₀为常数项，代表趋势值，d为差分次数。当d=0时，表示Y_t为稳态数列；d>0时，Y_t为非稳态数列，此时可借助差分的方式将之变为稳态数列。如d=1时，表示非稳态的Y_t数列经过一次差分后即成为稳态，d=2时则要经过两次差分，如此类推，且(1-B)^dy_t＝(1-B)^dY_t(2)预测。当一个模型经过设定、估计与诊断性检查等反复的修正过程而确定满意后，即可用之进行预测。现将ARIMA(p,d,q)模型写为：φ(B)Y_t＝θ(B)a_t 式中φ(B)=φ(B)(1-B)^d；当d=0时为稳态数列，而Y_t则可视为y_t＝(Y_t-μ)
令Y_t+1(l≥1)代表以t为预测起始点时，l期之后的观察值。亦即

Y_t+1＝φ₁Y_t+l-1+……+φ_p+dY_t+l-p-d+θ₁a_t+l-1-……-θ_qa_t+1-q+a_t+1

进一步以_t(l)代表Y_t+1的最佳预测值，即

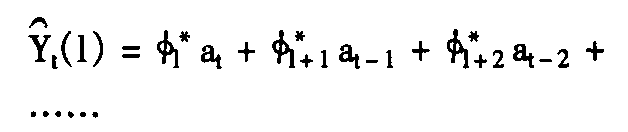
在a_t为常态分配，且Y_t,Y_t-1，…已知时，Y_t+1即是一个预期值为_t(l)，方差为Var[e_t(l)]的常态分配，亦即

Y_t+1～N{_t(l),Var[e_t(l)]}

由此，可利用下式进一步得出置信区间：式中α代表显著水准。当σ未知时，在大样本的情况下，可利用样本残差算出的标准差S_α替代，而得到近似的结果。