自回归移动平均ARMA

许多平稳的随机过程既不能用移动平均模型刻画，也不能用自回归模型刻画，因为它们都具有这两种模型的特性。(p,q)阶混合自回归-移动平均模型刻画了这些过程，记这种模型为ARMA(p,q)，由下式表示

y_t＝φ₁y_t-1+…+φ_py_t-p+δ+ε_t
-θ₁ε_t-1-…-θ_qε_t-q (1)

假定过程平稳，所以它的均值为常数

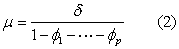
这给出了过程平稳的一个必要条件，即：

φ₁+φ₂+…+φ_p<1 (3)

容易证明

γ_k＝φ₁γ_k-1+φ₂γ_k-2+…+φ_pγ_k-p

(k≥q+1) (4)

这样
ρ_k＝φ₁ρ_k-1+φ₂ρ_k-2+…+φ_pρ_k-p

(k≥q+1) (5)
注意到过程的移动平均部分有q期记忆力，所以当k≥q+1时，自相关函数（或协方差）反映了自回归部分的性质。
引进新的记号是有用的，通常用向后位移算子来表示时间的滞后是非常方便的。每当算子作用于一个变量时，就使该变量的时期滞后1期。这样，Bε_t＝ε_t-1,B²ε_t＝ε_t-2,Bⁿε_t＝ε_t-n。利用这个算子，方程(1)的ARMA(p,q)过程可重写为：

(1-φ₁B-φ₂B²-…-φ_pB^p)y_t＝δ+(1-θ₁B-θ₂B²-…-θ_qB^q)ε_t (6)

或

φ(B)y_t＝δ+θ(B)ε_t

过程y_t平稳的充分必要条件为特征方程φ(B)=0,θ(B)=0的根都落在单位圆之外。