膜噪声membrane noise

在可兴奋细胞的细胞膜中，穿过细胞膜的电流量是跨膜电位的函数。但是，即使所有有关条件均不改变，穿过膜的电流量仍然有不断的微小起伏和波动，称膜噪声。

膜噪声

在可兴奋膜中，穿过细胞膜的电流是跨膜电位的函数，即是使所有有关的条件都不变，穿过膜的电流量仍不断有微小的起伏，这就是所谓膜噪声。
噪声的表示方法 有下列两种：
❶用噪声的振幅表征。通常以它对平均值变异的标准差来定。如属正态分布，起伏的68%振幅将位于±1标准差范围内，起伏的95%和99.7%分别在±2和±3标准差范围内。
❷用协变性函数或频谱表征。一个随时间而变的过程，标定其特征不仅需要知道关于它偏离平均值的振幅，还需要知道离差发生的快速程度。后者通常用协变性函数 (covariancefunction)或频谱来表示。由于在用计算机处理时，频谱更易计算，现在常用它来标定。
频谱和协变性函数的计算 方法如下： 先对记录进行傅里叶分析，从而将原来的时间函数转换为正弦、余弦权重表示的等价特征表示式。然后将和每一个频率成分联系的正弦余弦平方再取其平均值(即平方相加后被2除)。这个各种频率组分的平均平方数的集合组成原来过程的频谱。这种和记录相联系的频谱表征原来记录中起伏的快速程度，如果所测量的变数起伏、速率极快，其傅里叶分解将包含许多高频组分，因而其频谱的高频部分的值，相对而言将比较大。反之，如果原来的起伏很慢，高频权重将很小。通常取频谱振幅的对数对频率的对数作图，就比较容易看出频谱中所含信息。目前，频谱一般都用快速傅里叶变换计算。
协变性函数是频谱的傅里叶转换，它通常按下法计算。首先用快速傅里叶变换得到频谱，然后通过将不同频率的余弦波按其相应的频谱振幅权重相加，对频谱进行傅里叶变换，所得时间的函数就是所求的协变性函数c(t)。如果将这个协变性函数归一化，使它在t=0时的值为1，即为自相关函数。协变性函数指示一个信号的电流值和t秒后的值的相关程度。通常，无规过程的协变性函数从t=0时的极大值，随着时间的延长，逐渐光滑地降至0。如果衰变在1ms期间内出现，提示原来的起伏信号的相关延续1ms。
图中(A)是一个两端电网络，其端电压V和电流I假定由耗散和能量贮存单元供给，并假定V和I都是恒定的，去除平均值后，在网络N的端头的稳态起伏的电压波形△V(t)或电流波形△I(t)如图中B左方所示，图中(B)右方即为频谱的对数对频率的对数作图的结果。在I恒定时，其电压和电流频谱密度SV和SI为：
Sv(ω)=[△²(ω)/△ω]I=常数 (1)在电压恒定时

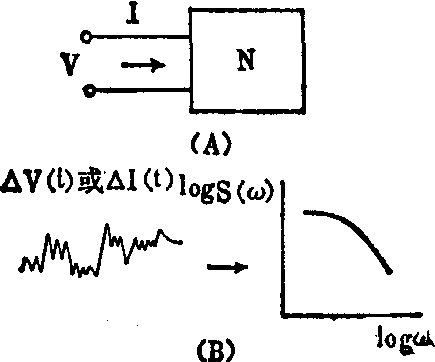
图(A)两端网络 (B)频谱对数和频率对数作图结果

S_I(ω)=[△I²(ω)/△ω]v=常数 (2)
S_V(ω)=S₁(ω)丨2(ω)丨²(3)
膜噪声的类别 在膜噪声中，除由带电荷粒子在导体中的热运动所引起的热噪声外，还有由于非平衡的离子系统引起的额外噪声。热噪声可用式(4)表示：
SE(ω)=4KTReZ (4)式中SE(ω)为电压频谱密度，ReZ为膜阻抗Z的实数部分，K为玻尔兹曼常数，T为绝对温度。按经典理论，这种起伏的频谱密度(除通过ReZ与频率相关外)和频率无关，因此又称为白噪声。
额外噪声包括以下几部分：
❶散粒效应噪声。如果有一些相同的事件，这些事件中任一个的发生都和以前发生的这些事件无关，所产生的噪声就称为散粒效应噪声。如果膜中离子通道的启闭是随机的，而且是相互独立的，那么，在电阻、电流和电压方面产生的起伏就可以作为散粒效应噪声来处理。它可以用式(5)来表示：
SI(ω)=29I (5)式中S₁(ω)为电流频谱密度，I为平均电流。
❷闪变噪声。这一类噪声的产生机理还不清楚。现用以指任何频谱密度随闪变(f-α)而变的噪声，其中α接近1。在膜研究中，首先研究的噪声就是这一种，它可以用经验式来表示：
S(ω)∝I^mf-¹ (6)式中S(ω)为频谱密度，m为常数，其值约为2。
❸猝发噪声。这是指一种不规则的、通常是非对称的、有如在铁导体中出现的Barkhausen噪声。
就可兴奋膜而言，有以下一些额外噪声：
❶和钾运转有关的f-¹噪声；
❷高频白额外噪声；
❸猝发噪声；
❹在突触后肌肉膜上有由递质释放引起的弛豫噪声；
❺和钾离子通道活动有关的散粒效应噪声；
❻和钠离子通道活动有关的散粒效应噪声；
❼和钠运转有关的f^-1噪声；
❽和膜的漏电有关的f-¹噪声；
❾代谢源活动的弛豫噪声。总之，对兴奋过程的研究、分析由离子通道的导电状态或开放数目的起伏引起膜噪声可以提供了解离子传导的一些微观机理所需的信息。此外，在膜噪声中钾、钠通道电导噪声是比较重要的，故应特别加以注意。
钾通道电导噪声 不论是在青蛙神经纤维的朗氏节或乌鲗大纤维膜上，在1/f噪声之外，还有弛豫型的散粒噪声组分θCE/(1+ω²θ²)，式中θ为时间常数，CE为电压频谱密度的比例常数。在大纤维内部用四乙胺、低钾离子或氟化铯溶液灌注后弛豫噪声消失。在青蛙神经纤维的朗氏节处外加四乙胺后，这个噪声成分发生改变，由此可推断它是和钾运转系统有关的。
关于通道启闭的可能方式中有所谓“多状态”模型和“双状态”模型之分。
多状态模型是指通道的电导可以有几个数值。考虑的出发点是N个独立的通道遵循泊松分布。按照Hodgkin和Huxley的假设，每个通道的电导由它的亚单位的状态所定，亚单位的数目x待定。按原来Hodgkin和Hu-xley的假设，当x=4时，且每个亚单位的假定状态和其它亚单位的无关，则其构象变化决定于膜电位，由速率常数α1和β1表征，它们分别反映电静息状态到激活状态以及其逆过程的情况。对于给定数目i的亚单位，在这两个状态之间用上述速率常数变换，结果得到散粒噪声型的状态频谱密度S_i(ω)为：

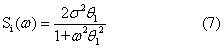
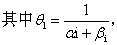α1为膜外至膜内的速度常数，θ1为膜内至膜外的速度常数，σ2的值没有标定。对于所有的x个亚单位，总的电导频谱为个别频谱之和与通道数目(N)的积。在这种模型中，虽然每个亚单位的状态只有两种，可是通道的状态却因x个亚单位状态组合的不同，可以有多种。
在另一种模型中，假定每个通道根据其亚单位的状态或处于开放状态 [h（全）、电导为r]或处于关闭状态[0（无）、电导为0]。每个亚单位也只能存在于两种状态之一中，或者不活动、或者活动。每个亚单位状态随转换的速率常数和所联系的时间常数而定。P∞(h)i是第i个亚单位处于活动状态的概率，在稳态时是常数，且由膜单位决定。这样，x个亚单位结构的总数可以有2x个，而只有在这种状态时，通道才是开放的。
从理论上分析，可以从比较不同膜电位和不同温度时得到的钾噪声的时间常数θ来分辨钾通道相应于那一种模型。但由于各种技术上的困难，目前尚不能得到最终的结论。从噪声分析，除可以探讨离子通道的启闭方式外，还可以求得所观察区域的通道数N和每个通道的电导r。虽然迄今这方面的结果都还是初步的，但是可以推测从膜噪声的研究中可以获得的情况。
钠通道电导噪声 假定钠通道是双状态的，根据Hod-gkin和Huxley的假设，每个钠通道由x和y两种亚单位控制。假设其数目分别为α和β。对于x亚单位则为
α_i＝α_m,β_i＝β_m,P(h)_i＝m∞
对于y亚单位则为
α_s＝αh,β_s＝βh,P(0)_j＝hω
那么，可以达到活动状态的数目为(x+1)(y-1)-1。如果x、y的数目为Hodgkin和Huxley所假设的，分别为3和1，则对于N个独立的钠通道，电导频谱为[SgNa(f)]

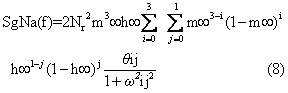
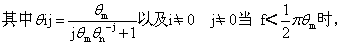频谱是白的，然后按1/f2减少。到f>1/2πθm时又可能变白。 在频率更高时出现三个“峰”。 然后当f>>3/2πθm时，它再随1/f²减小。
按式(8)，由M过程引起的电流方差为：
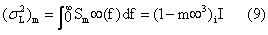　其中i为单通道开放时的电流，I为穿膜平均总电流。
如果通路开放有几种中间状态，例如和m过程有关的亚单位可以分别独立改变状态，有一个亚单位处于它的“关闭”状态时，通道的电导就减为这个亚单位处于 “开放”状态的K倍(0　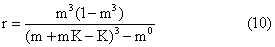只要K>0.05，实验结果与第一种假设计算结果有较大的差异。从实际测得的结果来看，K<0.03，也就是说，通路的启闭基本上是全或无的。