置信区间confidence interval
又称置信距。统计推断上,在一定概率保证下,所估计出的总体参数可能所处的一个范围或区间。以样本平均数作为总体参数的估计值,仅是一种点的估计,其中并未考虑试验误差的影响。较为合理的表示则为在一定概率保证下的置信区间,所以,它是参数的区间估计值。平均数的置信区间可用 -ta·S
-ta·S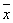 ~
~ +ta·S
+ta·S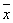 表示。
表示。
置信区间range of confidence
亦称可信区间,是用样本统计数(如X)估计总体参数(如μ)的可能范围。如以样本均数X估计总体参数μ时,因存有抽样误差,只能以一定的把握度对μ进行区间估计。通常以95%和99%两个概率水准作区间估计,称95%或99%的置信区间,其估计公式是:
95%的置信区间 μ=±t0.05(v)S
99%的置信区间 μ=±t0.01(v)S式中S代表标准误,t0.05(r)和t0.01(r)是自由度为v时在μ=0.05和0.01水平上的t值。可信区间的两个界值,称可信限。
置信区间confidence interval
参见“区间估计”条。
置信区间Confidence Interval
由样本统计量所构造的总体参数的估计区间,即该参数的真实值落在测量结果周围的可能性。
置信区间
见“参数估计”条。
置信区间
亦称“置信域”。为了估计随机变量总体分布的一个未知参数θ,找出一个区间[ 1
1 2],如果区间包含参数θ的概率大于或等于预先给定的值1-α( 0<α<1 )这个区间称为θ的置信区间。其中θ1和θ2分别称为θ的置信上限和置信下限。( 1-α)称为置值度、置信系数或置信概率。
2],如果区间包含参数θ的概率大于或等于预先给定的值1-α( 0<α<1 )这个区间称为θ的置信区间。其中θ1和θ2分别称为θ的置信上限和置信下限。( 1-α)称为置值度、置信系数或置信概率。
置信区间confidence interval
设总体分布有一参数β,根据样本计算其估计量为β,对于给定的正数α(0<α<1),找出另一正数δ,使
P( -δ≤β≤
-δ≤β≤ +δ)=1-α
+δ)=1-α
 -δ,β+δ]称为β的100(1-α)%置信区间。其中1-α称置信度(degree of confidence),常用百分数表示为100(1-α)%。上式表明,由样本观测值构造的置信区间包含真值β的概率为1-α,所以[
-δ,β+δ]称为β的100(1-α)%置信区间。其中1-α称置信度(degree of confidence),常用百分数表示为100(1-α)%。上式表明,由样本观测值构造的置信区间包含真值β的概率为1-α,所以[ -δ,
-δ, +δ]又称为β的区间估计式。
+δ]又称为β的区间估计式。由最小二乘法得到的是回归方程系数的点估计式,进一步推导出的系数方差和扰动项方差也都是点估计式。仅由点估计式无法判断其可靠程度,而区间估计式则补充了这一不足。区间估计式指出了真值落在该区间内的概率。
置信区间也用于[假设检验],称置信区间法。如果原假设给出的β值落在置信区间外,那么我们就拒绝原假设,接受备择假设。
置信区间confidence interval
由样本值对总体进行估计时,在一定置信水平下的估计值的范围。亦称“置信域”。由美国统计学家奈曼(Neyman,J.)提出。在统计检验中,当估计一个未知的参数的值时,一般通过样本的观察值给出一个范围,使得这个范围能按照足够大的概率(给定的)包含所要估计的参数,这个范围就称为置信区间。置信区间的确定,可根据样本的观察结果来确定θ1和θ2。当θ1和θ2对于给定的显著水平θ(θ<1=满足
θ1≤θ0≤θ2
则P (θ1 ≤θ0≤θ2) =1-αθ0为待估计的参数;区间(θ1,θ2)为置信区间; θ1和θ2分别为置信下限和置信上限;1-α为置信系数,或置信概率,表明区间估计的可靠性,它是区间估计的可靠概率;α为显著性水平,表明区间估计的不可靠概率。
置信区间confidence interval
亦称“置信间距”。在某一置信度时,总体参数所在的区域距离或区域长度。置信区间越长,置信水平越高。
置信区间
亦称“置信间距”。指在某一置信度时,总体参数所在的区域距离或区域长度。置信区间的两个端点值称为置信界限。置信度,又称置信水平,其值为1-α,α为显著性水平。
- 哗啦啦是什么意思
- 哗啦杨是什么意思
- 哗啦棒槌是什么意思
- 哗啷啷是什么意思
- 哗啷啷声(硬币)是什么意思
- 哗啷啷(啷)是什么意思
- 哗啷棒儿是什么意思
- 哗喇是什么意思
- 哗喇喇是什么意思
- 哗嘲是什么意思
- 哗噪是什么意思
- 哗嚣是什么意思
- 哗备是什么意思
- 哗强之人为人伪增籍面是什么意思
- 哗徒反复变诈案是什么意思
- 哗怒是什么意思
- 哗戏是什么意思
- 哗才是什么意思
- 哗拇是什么意思
- 哗拉是什么意思
- 哗拉拉是什么意思
- 哗枚是什么意思
- 哗楞楞是什么意思
- 哗溃是什么意思
- 哗滚是什么意思
- 哗然是什么意思
- 哗然嘲笑是什么意思
- 哗然而怒是什么意思
- 哗疑是什么意思
- 哗笑是什么意思
- 哗耳是什么意思
- 哗言是什么意思
- 哗讦是什么意思
- 哗词是什么意思
- 哗诛是什么意思
- 哗酒是什么意思
- 哗门吊嘴是什么意思
- 哗闹是什么意思
- 哗骇是什么意思
- 哘是什么意思
- 哙是什么意思
- 哙伍是什么意思
- 哙参珠是什么意思
- 哙哙是什么意思
- 哙等是什么意思
- 哙等伍是什么意思
- 哚是什么意思
- 哚哉是什么意思
- 哚啘是什么意思
- 哛是什么意思
- 哜是什么意思
- 哜㗖是什么意思
- 哜了咯生是什么意思
- 哜咕是什么意思
- 哜咨是什么意思
- 哜咯是什么意思
- 哜咯啷是什么意思
- 哜哜是什么意思
- 哜哜哝哝是什么意思
- 哜哜嘈嘈是什么意思