罗尔中值定理lu-oar zhongzhi dingli

若函数f (x)满足条件❶在闭区间 [a,b ]上连续；
❷在开区间 (a,b)内可导；
❸在这区间端点的函数值相等，即f (a) =f (6)，则在 (a,6) 内至少存在一点c，使得f ′ (c) =0.

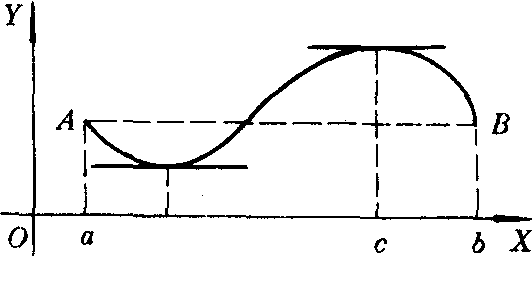
罗尔定理的几何意义如图所示.它表明，若连续曲线y=f (x)的弧AB上处处具有不垂直于x轴的切线，且两端点的纵坐标相等，则这弧上至少存在一点，使曲线在该点处的切线平行于X轴.
罗尔定理的三个条件都是重要的，如缺少其中的任何一个，定理的结论将不一定成立.例如，函数f (x)=x满足条件❶,
❷，但f (0) ≠,(1),f′ (x)=1，故结论不成立. 当然，也容易举例说明，即使定理的条件不全具备，也可能存在这样的点c，使f ′ (c) = 0.所以定理的条件是充分的，但不是必要的.