网络分析network analysis

用网络形式描述一个工程项目或组织计划问题，求其最优解的技术。其理论基础是图论。网络的基本成分是点（称为顶点或节点）和连接点的有向线段（称为弧）。对每一条弧给予物理含义，并赋予一个数值，称为该弧的权，权可以表示距离、时间、费用、流量等。
1955年，哈里斯(T. E. Harris)研究铁路网最大通过能力时首先提出在一个给定网络上求某两点间最大运输量问题。1956年福特(L. R. Ford)和富尔克森(D. R. Fulkerson)给出了算法，从而建立了网络流理论。20世纪60年代以后，由于电子计算机的发展，大规模网络分析问题的求解成为可能，使网络分析广泛应用于大型灌溉系统，计算机网络、电缆电视网络、运输系统、库存与商品分配和计划管理等方面。网络分析的内容很多，常见的有最短路问题、最大流问题、邮递员最佳路线问题及网络计划技术等。
最短路问题 决定网络中从指定一点到其余任意一点之间的最短距离及其所走的路线。“距离”是广义的，可理解为时间，费用等，指定的一点称为始点，到达点称为终点。从i点到j点的距离记为d_ij，当i点到j点没有线段相连时，d_ij＝∞。最短路问题可化为动态规划问题来求解。1959年狄克斯特拉(E. W. Dijk-stra)提出了求解最短路问题的标号法，当网络中各弧的权是正数时，它不仅可以得到始点至终点的最短距离和最短路线，而且还得到始点到网络中任一点的最短距离和最短路线，其基本方法是：先从始点V₁开始，由于它到自身的距离为零，所以记上固定标号P(V₁)=0，其余各点记为临时标号，T(V_j)=∞,j=2,3，…，n。然后从固定标号点出发，考虑固定标号点i箭头所指的节点j，当找到V_i到V_j点的最短路线时，把V_j点改为固定标号。重复上述步骤，直到终点被标上固定标号时，即找到始点到终点的最短距离和最短路线，其计算公式是：

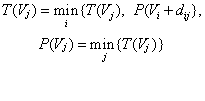
最大流问题 当某种物质、信息、能量通过给定的网络时，在网络系统运行状态稳定的情况下，决定从始点可能发出的最大流量（或终点可能收到的最大流量）及各弧应负担的通过流量。许多实际系统的网络中，都包含了流量问题。如公路交通网中有车辆流，供水(油、气)的网络中有水流。网络中每一条弧(V_i,V_j)最大可能通过的流量称为该弧的容量，用C(V_i,V_j)表示，或简记为C_ij; 在系统的运行中，实际通过的流量用f(V_i,V_j)来表示，或简记为f_ij。要求0≤f_ij≤C_ij，当f_ij＝C_ij时，称该弧(V_i,V_j)为饱和弧，否则称为非饱和弧。始发点用V_s来表示，终点用V_t来表示，其余各点称为中间节点。中间节点不储存流量，即流入每个中间节点的所有流量之和等于流出的所有流量之和。一个网络的最大流问题可用线性规划模型来描述，其决策变量为各弧的流量f_ij，目标函数是始发点发出的流量之和最大（或终点接收到的流量之和最大），约束条件包括： ❶弧的容量约束，即各弧的流量要小于或等于各弧的容量；
❷中间节点平衡约束，即各中间节点流入流量之和等于流出流量之和；
❸变量的非负约束。
对于一个复杂的网络最大流问题，虽然可用线性规划模型来描述，但其决策变量数和约束方程数都很大，求解比较麻烦。1962年，福特-富尔克森(Ford-Fulkerson)提出了求解网络最大流的标号法。其基本原理是从一个零流（即每条弧的流量都为零）或可行流（即各弧的流量要满足上述的三组约束条件）出发，在网络中寻找一条从始点到终点可以增加流量的路径，称为增广路。与这条路方向一致的弧，称为正向弧，方向相反的弧称为反向弧。非饱和的正向弧和流量非零的反向弧都可以作为增广路上的弧。然后调整增广路上各个弧的流量，使通过这条路上的流量尽可能增加。重复这个过程，直至找不到增广路为止。此时就获得网络上各个弧应负担的流量，从始点发出的各弧流量之和（或终点接收到的流量之和）就是该网络的最大通过流量。用标号法求得网络的最大流时，同时获得了影响这个网络流量增大的关键部位，若希望扩大网络的流量，必须首先扩大关键部位上各弧的容量。
最大流问题在农业上有很多应用场合，如美国虫害防治机构，通过对历年蝗虫迁移路径的广泛调查，绘制了蝗虫迁移网络图。各弧的容量是预计飞经该路径的蝗虫最大数目。因而把问题概括为求最大流问题。因此，只须向各关键部位喷撒足够的农药，即可保证杀死蝗虫，且农药化费又最少。
邮递员最佳路线问题 一个邮递员如何选择最短路线，走遍他所负责的每条街道，完成邮递任务后回到邮局。这个问题是中国数学家管梅谷先生在1962年首先提出的，所以在国际上称为中国邮递员问题。解决这个问题可采用奇偶点图上作业法。
网络计划技术 网络分析方法在各种工作任务的组织安排和计划管理中的应用，统称为网络计划技术其主要内容有关键路线法，计划评审技术等。1956年美国杜邦公司在制订工厂设备维修计划时，使用关键路线法CPM(Critical Path Method)。1958年美国海军武器局，在研制“北极星”导弹计划时，使用计划评审技术PERT (Program Evaluation and ReviewTechnique)。1965年中国数学家华罗庚教授，在中国推广应用“统筹方法”。网络计划技术广泛应用于大型工程项目施工、综合性科学研究、建筑施工和大型设备维修计划的制订等方面。
网络计划技术的主要方法步骤包括： ❶任务的分解和分析。把一个工程项目分解为若干工序，然后确定每个工序所需时间和各工序之间的先后关系。将分析的结果汇编成如下形式的表格：

网络图

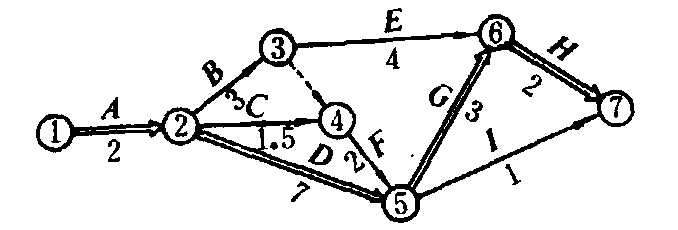
对不需要人力和物力，只需要时间的过程，如水泥浇灌后的固化时间，也当作一个工序进行安排。
❷绘制网络图。以下图为例来说明。图中箭头表示工序。圆圈（顶点）表示事项，事项表示一个工序开始或结束的时刻。圆圈中的数字是事项的编号。工序代号写在箭杆上方，工序时间写在箭杆下方。一支箭杆上的两个事项不能同另一支箭杆上的两个事项完全相同。有时，为表示工序之间的先后关系，需引入虚工序，它不代表任何实际活动。如图中用
❸→
❹表示工序E的紧前工序是B，而工序F的紧前工序是B和C。
❸网络图中的参数计算。参数计算的主要目的是找出工程中的关键工序和关键路线。工序时间是指完成任务所需的时间，用T(i,j)表示。当难以准确确定工序所需时间时，可采用三点估计公式计算：

式中 M为工序时间的估计值，a为最乐观的工序时间，b为最悲观的工序时间，c为最可能的工序时间。事项的最早可能时间用TE(j)表示，计算公式是：

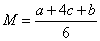
TE(1)=0,TE(j)=max{TE(i)+T(i,j)}

j=2, 3，…，n

其中n为最终事项的编号，TE(n)为工程的总完工期，i为指向事项j的各事项编号。如图中，TE(1)=0,TE(2) =2, TE(3) =5，而TE(4) =max {TE(3)+T(3,4),TE(2)+T(2,4)}=max {5,3.5}=5，…，TE(7)=14。事项的最迟必须时间用TL(i)表示。计算公式是TL(n)=TE(n), TL(i)=min{TL(j)-T(i, j)}, i=n-1,n-2，…，1，在图中，TL(7) =14,TL(6)=14-2=12,TL(5) =min {12-3,14-1} =9,TL(4)=9-2=7，…，TL(1)=0。事项时差是事项最迟必须时间与事项最早可能时间之差，用R(i)表示，R(i)=TL(i)-TE(i)。图中，R(4)=TL(4)-TE(4)=7-5=2。图中各事项的事项时间参数计算结果如下表所示：

事项编号	1	2	3	4	5	6	7
TE(i) TL(i) R(i)	0 0 0	2 2 0	5 7 2	5 7 2	9 9 0	12 12 0	14 14 0

工序最早可能开工时间用TES(i,j)表示。工序的最早可能完工时间用TEF(i,j)表示。计算公式为TES(i,j)=TE(i),i=1,2，…，n,TEF(i,j)=TES(i,j)+T(i,j)。工序最迟必须开工时间用TLS(i,j)表示，工序最迟必须完工时间用TLF(i,j)表示。计算公式为TLS(i,j)=TL(j)-T(i,j),j=n,n-1，…，1,TLF(i,j)=TLS(i,j)+T(i,j)。工序总时差是指保证总完工期为TE(n)情况下，允许某一工序(i,j)灵活松动的时间范围，用R(i,j)表示。计算公式为R(i,j)=TLS(i,j)-TES (i,j)。工序的局部时差是指保证紧后工序最早可能开工时间的情况下，允许某一工序(i,j)灵活松动的时间范围，用r(i,j)表示。计算公式为r(i,j)=TE(j)-TEF(i,j)。图中各工序的时间参数计算结果如下表所示：

工 序	TES(i,j)	TEF(i,j)	TLS(i,j)	TLF(i,j)	R(i,j)	r(i,j)
A(1,2) B(2,3) 虚工序(3,4) C(2,4) D(2,5) E(3,6) F(4,5) G(5,6) H(6,7) I(5,7)	0 2 5 2 2 5 5 9 12 9	2 5 5 3.5 9 9 7 12 14 10	0 4 7 5.5 2 8 7 9 12 13	2 7 7 7 9 12 9 12 14 14	0 2 2 3.5 0 3 2 0 0 4	0 0 0 1.5 0 3 2 0 0 4

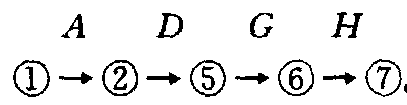总时差为零的工序称为关键工序，其余工序为非关键工序。由关键工序组成的从始点到终点的路称为关键路线。图中的关键路线为：。关键路线是网络图上的最长路。关键路线上各工序时间之和等于工程的总完工期。有时可能存在长度相等的多条关键路线。
❹工程在预定时间内完工的概率问题。采用三点估计法计算工序时间时，总完工期是一个不确定值。工程完工时间可近似地认为是一个服从以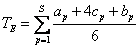(P包括一条关键路线上的各工序)为均值，以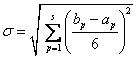为均方差的正态分布随机变量。当关键工序的平均工序时间和σ为已知时，可算出工程在规定完工时间的概率，或计算出具有一定概率值的工程完工时间。计算公式为T_k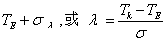＝。其中T_K为规定的工程完工时间；T_E为工程平均完工时间，即各关键工序平均工序时间的总和；λ是σ的系数。
❺网络计划的优化。逐步调整网络计划，在各种资源约束下，寻求工期最短的方案；或在工期一定的条件下，寻求资源投入量最少的方案。对一个工程项目缩短完工期，除在关键工序加强组织安排外，一般需增加资源或采用加班的办法，这势必要增加工程的费用，如何确定在哪些工序增加费用来缩短时间，并使增加的费用最少。这是另一类网络计划的优化问题。解决这类问题，首先要分析各关键工序缩短单位时间与增加费用之间的关系，若能找到时间与费用的函数关系，则可应用数学规划加以计算，否则可从正常时间的网络计划出发，选择缩短单位时间所需费用最小的工序开始，逐步调整和缩短工期，直至获得比较满意的方案为止。
❻网络计划的实施与调整。

网络分析

输入激励与网络元件参数已知时，计算网络响应的方法。电网络的分析又称电路分析。网络分析常涉及对激励信号本身的研究和对网络本身结构的分析。最基本的计算法则是基尔霍夫定律。

网络分析

在图论的基础上形成的一种优化方法。主要研究最大流问题、最短路问题和最小费用最大流问题等。

网络分析Network Analysis

涉及确立和度量个人、团队、组织与信息技术之间的关系和流程。在网络分析图上，每个人、团队、组织用一个交点代表，用线连接这些交点，则可用图形表示网络上交点之间的相互关系。在一个团队、部门、分支机构或组织内部，网络分析很重要，因为网络分析图的构建可以简要说明这些交点的相对重要性，即可以通过测量一个交点的集中度或突出程度来确定其在网络中的重要性。

网络分析

network analysis