统计估计statistical estimation

利用样本资料对总体参数进行估计，或在有一定相关关系的随机变量之间，按一定的准则，根据一些随机变量对另一随机变量作最佳估计与预测。设总体x的分布函数为F(x;θ)，其中x₁为x的观测值，θ为未知参数，θ的取值范围Θ为参数空间。 由子样x₁,x₂，…，x_n建立不带有未知参数的统计量f(x₁,x₂，…，x_n)对未知参数θ做出最佳估计，即为参数估计。参数估计分为点估计和区间估计两类。称f(x₁,x₂，…，x_n)为θ的估计量，记作。对于子样观测值(x₁,x₂，…，x_n)，称t=f(x₁,x₂，…，x_n)为θ的估计值，建立统计量＝f(x₁,x₂，…，x_n)作为θ的估计量，即为参数θ的点估计。如果随机变量x的分布函数F(x;θ₁，…，θ_k)中有k个不同的未知参数，则要由子样x₁,x₂，…，x_n建立k个不带有任何未知参数的统计量作为这k个未知参数的估计量，常记作₁₂，…，_k。
鉴别估计量好坏的常用标准有：
❶无偏性：设是θ的估计量，当满足E()=θ时，称θ为θ的无偏估计；
❷有效性：若θ的某估计量₁对于除₁外任何其他的估计量均有D(₁)≤D()，则称₁为对θ最有效（具有最小方差）的估计量。
常用的点估计方法有：
❶矩估计法：即用子样矩作为总体矩的估计；
❷最大似然估计法：由总体分布密度函数f(x;θ)，按样本观察值构造似然函数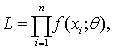选取使L(x₁，…，x_n;(x₁，…，x_n))=SUPL(x₁，…，x_n;θ)成立的(x₁，…，x_n)作为θ的估计；
❸贝叶斯估计法：依赖于θ的先验分布的估计方法。还有序贯估计法、最小平方估计法等。
设总体x的分布函数F(x;θ)中的θ为未知参数，由子样x₁，…，x_n建立两个统计量T₁(x₁，…，x_n)及T₂(x₁，…，x_n)，并满足T₁2,[T₁,T₂]为随机区间。区间估计的表述为：设α为一给定常数(0<α<1)，若P{T₁≤θ≤T₂}=1-α成立，并用该随机区间作为θ的估计，则[T₁,T₂]是参数θ的置信水平为1-α的区间估计。α为显著性水平，T₁、T₂分别为上、下置信限。