线积分

又称“曲线积分”。积分区间由直线段推广到曲线上的定积分。如果曲线是无向的称为第一型曲线积分；如果曲线是有向的称为第二型曲线积分。用于求曲线的质量和变力沿曲线作功等问题。

线积分

一个位置的向量函数F沿路线C的线积分用下式表示：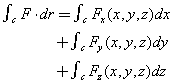

其中Fx,Fy,Fz是F沿坐标轴的标量分量。假设路径C是一条曲线，它至少是分段光滑的，并且对每一光滑部分，用形如x=xp,y=y(p),z=z(p)的方程以参数形式定义。在这种情况下，线积分可用下式计算：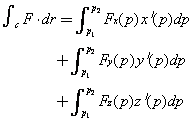

其中p1,p2是路径C或其一个光滑段的端点的参数值，于是积分转化为普通的定积分。
当C是一封闭的曲线时，线积分叫回路积分，并以记号
φF·dr表示
线积分的一些物理应用如下：如果F是力，线积分就是一物体沿曲线C移动时所作的功；如F是流体的流速，线积分就是流体沿曲线的环流等等。