简谐振动表示法jianxie zhendong biao shi fa

简谐振动常用数学解析式、振动曲线、旋转矢量三种方法表示。
❶数学解析式表示：简谐振动的动力学方程为d²x/dt2+ω02x=0，运动学方程为x=Acos(ω0t+ᵠ)。由此得到简谐振动的速度v=-ω0Asin(ω₀t+ᵠ)，加速度a=-ω02Acos(ω0t+ᵠ),ω0A为简谐振动的最大速度的绝对值，叫做速度幅，用v_m表示，ω02A为简谐振动的最大加速度的绝对值，叫做加速度幅，用a_m表示。
❷振动曲线表示：表示振动物体相对平衡位置的位移随时间变化的关系曲线(图1)，称为简谐振动曲线，它是以x为纵轴、t为横轴的余弦函数（或正弦函数）曲线，也称x-t曲线。振动曲线能直观地表示出物体相对于平衡位置的位移随时间变化的情况，以及振幅A、周期T的物理意义，并且可据此求出初位相ᵠ。简谐振动的速度、加速度随时间的变化关系也可作出相应的v-t曲线、a-t曲线，一般将这三种曲线作在一起，便于直观地比较位移、速度、加速度三者的关系。

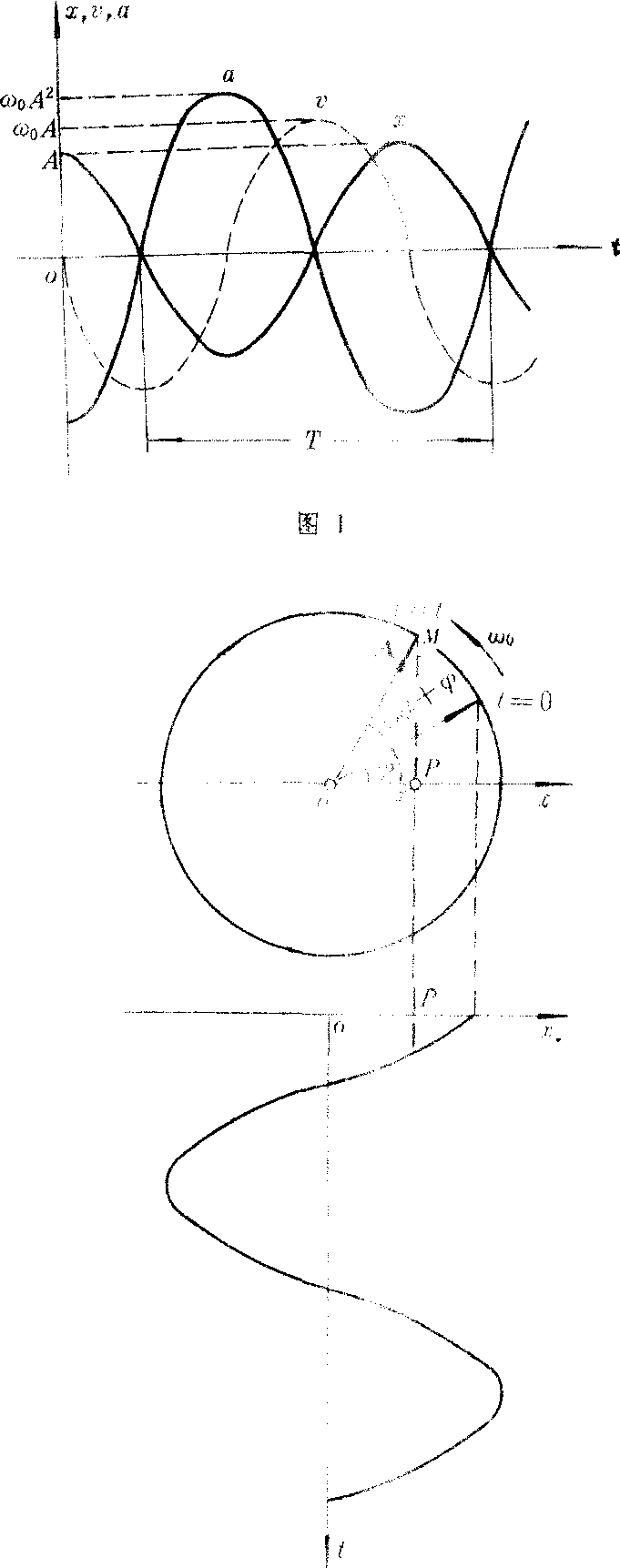
图2

❸旋转矢量表示：对于某简谐振动x=Acos(ω₀t+ᵠ)，可如图2所示，取ox坐标轴，从原点o作一矢量A，使其长度等于简谐振动的振幅A;t=0时矢量A与ox轴夹角等于振动初位相ᵠ；并使矢量A以大小等于振动圆频率ω0的角速度沿逆时针方向匀速旋转，这个矢量就叫做旋转矢量。在任一时刻t矢量A与ox轴的夹角为ω0t+ᵠ，恰等于简谐振动在该时刻的位相。矢量A在ox轴上的投影为x=Acos(ω0t+ᵠ)。显然，旋转矢量A的矢端M在x轴上的投影点P作简谐振动，并且就是给定的简谐振动。旋转矢量A以ω0匀速旋转一周，振动物体就完成一次全振动，所以T=2π/ω0。因此投影点P就在作以o点为平衡位置，|A|为振幅，2π/ω为周期，ᵠ为初位相的简谐振动。图2同时给出了旋转矢量表示法与x-t图的对应关系。另外，旋转矢量A的矢端M的速度和加速度在ox轴上的投影，可表示此简谐振动的速度和加速度。矢端沿圆周运动的速率为ω0A，由图3可知，t时刻矢端速度与ox轴夹角等于(ω0t+ᵠ+π/2)，矢端速度在ox轴上的投影为ω0Acos(ω0t+ᵠ+π/2)，恰为此谐振动的速度。矢端沿圆周运动的加速度即向心加速度大小为ω20A,t时刻加速度与ox轴夹角为(ω0_t+ᵠ+π)，它在ox轴上的投影为ω20Acos(ω0_t+ᵠ+π)，恰为此谐振动的加速度。以上就是对于给定的简谐振动的旋转矢量表示法。矢量A的矢端M在任何位置上的位移、速度、加速度在ox轴上的投影，就等于作谐振动的P点在相应位置上的位移、速度、加速度。要注意，以简谐振动的平衡位置o点为圆心、振幅A为半径所作的圆，通常叫作简谐振动的参考圆，M叫参考点。参考点和旋转矢量本身并不作简谐振动，而是投影点作简谐振动。参考圆和旋转矢量是用来直观地研究谐振动的几何方法，它不仅可以帮助我们形象地了解简谐振动各物理量之间的关系，而且可以方便地用矢量相加法来研究振动的合成。

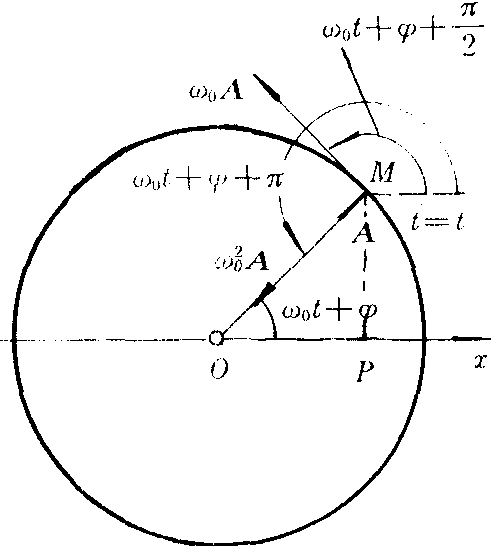
图 3