等价关系

指两个或两个以上的语言成分相互包含的关系，如同义词是语义上的等价关系。句式转换是句子间或表层结构间的等价关系。

等价关系dengjia guanxi

若r是非空集合A上的一个关系，当且仅当r对于任何的a,b,c∈A，满足下列条件时，则称r是A上的一个等价关系：
❶反身性： ara;

❷对称性： arb⇒bra;

❸传递性： arb且brc⇒arc.
实数集R上的关系“=”就是R上的一个等价关系.这是因为对于任意的a,b,c∈R，有：
❶a=a;

❷a=b⇒b=a;

❸a=b且b=c⇒a=c.
不难验证，实数集R上的大于关系“>”或小于关系“<”都不是R上的等价关系.如果r是A上的等价关系，通常用符号“～”来代替r.

---

等价关系dengjia guanxi

具有反身性（自身性）、对称性、传递性的关系.
若对任意x∈X，都有 (x,x)∈R，则R称为X上的一个自反关系，或称R具有自反性 （反身性）.
例如，X= { 1,2,3,4} ,I x是X上的一个自反关系. R= { (1,1),(2,2),(3,3),(4,4),(1,2)}也是X上的一个自反关系. 对任意集X,Ix具有自反性. 事实上， R是自反关系当且仅当Ix⊆R.
若对任意x,y∈x，当 (x,y) ∈R时，必有 (y,x)∈R，则称R是X上的一个对称关系，或称R具有对称性.
若对任意x,y,z∈ Z，当 (x,y) ∈R，且 (y,x)∈R时，必有 (x,z) ∈ R，则称R是X上的一个传递关系，或称R具有传递性.
对任意集X,I_x同时具有自反性、对称性、传递性，因此I x是集X上的一个等价关系. 同样，X×X也是X上的等价关系. 又如，说X为平面上三角形集，则相似关系、全等关系都是X上的等价关系.设Y是平面上的直线集，认为直线l与自身平行，则平行关系是Y的一个等价关系，而垂直关系只是Y上的一个对称关系.
设m (>1)是任一正整数，则任意整数n，必存在唯一的一对整数q,r，适合n=qm +r,O≤r1 =q₁m+r,n₂ =q₂m+r,0≤r0,n₁,n₂符合同余关系，记作n₁≡n₂ (modm).
容易证明模m的同余关系是Z上的一个等价关系，并且a≡b(modm)当且仅当m|(a -b).
当R是X上的一个等价关系，a∈X，令

[a]_R ={b| (a,b) ∈ R}

即所有与a符合等价关系R的元的集合，称为a形成的R等价类.
可以证明，如果R为X上的等价关系，(a,6) ∈ R，当且仅当 [a]_R [b]_R. 并且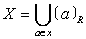，对任意a,b ∈X,(a,b)R , 则 [a]_R∩ [b]_R =φ.
当A =∪A_i ，对任意i∈I,A_i≠ φ;A_i∩A_i =φ,i∈I_i≠j;i,j∈I ，则称 {A_i},i∈I是A的一个划分. A上的任何一个等价关系R决定A的一个划分.
例如，Z上的模m同余关系对Z的划分是

Z =[0] ∪ [1] ∪ [2]∪ ……∪ [m-1]

式中[i]表示所有形如km+i,0≤i反过来，A的任一划分也确定A上的一个等价关系R，因为“属于同一子集”是A上的一个二元关系，且是一个等价关系.