空间圆的方程kongjian yuan de fangcheng

球面与一平面相交，它们的交线必是圆，于是得空间圆的普遍方程是

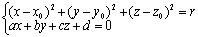
空间圆C，以空间任一点O为原点建立空间直角坐标系，使XY面与圆C所在平面平行。设圆C的圆心C的坐标为 (c₁,c₂,c₃)，半径为r，过C作CX′ 和CY′ 分别与X轴及Y轴平行。设P是圆上任一点，又∠X′ CP=θ，则向量形式的圆C的参数方程是P=C+rP (θ) (0<θ<2π)，此处G= {c₁,c₂,c₃)。化成坐标形式，即得x=c₁ +rcosθ,y=c₂+rsinθ,z=c₃ (0<θ≤2π)。