示踪动力学

机体内各种物质经常处于摄入、排出、合成、分解、转移等运动过程中。要了解各种物质的运动规律及其在疾病状态下的变化，有时不能简单地依靠定量或定位分析，而需用核素示踪法观察标记物的动态变化，并通过数学运算求出有关的动力学参数。这类工作的理论和方法称为示踪动力学。示踪动力学不仅有助于了解生理活动规律及疾病发生发展的规律，而且对疾病的诊断也有较大潜力。药物的示踪动力学研究对阐明药物在体内的运动规律有重要作用，被称为药物动力学或药代动力学，已成为药理学的一个重要分支。
代谢区或代谢库 同一物质可分布在不同解剖部位。如果它在几个解剖部位中交换迅速，各向同性，运动规律相同，则示踪动力学就认为对该物质来说，这几个解剖部位属同一代谢区或代谢库。物质在代谢区中的总量称为库大小，单位是m mol或其他质量单位，液体物质也可用体积单位。反之，若几个解剖部位中某物质的运动规律不同，则应视为不同的代谢区。多数物质都有二个或更多的代谢区，各区间常有单向或双向的转运，形成一个系统。最常见的是双库或三库系统。
动力学参数 示踪动力学采用一系列与速度有关的量来表示物质运动的特征。一般可分为三类：
(1)表示绝对速度的参数： 最常用的有更新速率、输入速率、输出速率、产生速率、排除速率及清除率等。更新速率表示某代谢区中某物质单位时间更新的量。输入速率和输出速率表示某代谢区在单位时间内输入或输出某物质的量。产生速率表示某代谢区在单位时间内从系统外获得某一物质的量。排除速率表示某种物质在单位时间内从某代谢区排除至系统外的量。以上各种速率的单位都是单位时间内的质量数。对体液内某种物质的清除速度，通常以单位时间内该物质从多少体积的体液中被清除来表示，称清除率。用绝对速度表示的动力学参数比较直观，但不能直接反映某一变化对代谢库影响的大小。
(2)表示相对速度的参数： 即各种速率常数。速率常数表示单位时间内某一变化的量相当于库大小的百分之几，故等于速率被库大小除。不同的速率有相应的速率常数，最常用的有更新速率常数（亦称部分更新速率）、输入速率常数、输出速率常数等。
(3)用时间表示的参数： 最常用的是更新时间及半更新时间。前者表示某代谢区中某物质更新的量相当于库大小所需的时间，后者则表示更新量相当于库大小的一半所需的时间。更新时间等于更新速率常数的倒数，半更新时间则等于0.693乘更新时间。
示踪动力学求解动力学参数的一般步骤 首先根据已有的生物学知识选择物理模型。物理模型可分两大类。一类为代谢区模型或确定性模型，要求设定系统中有若干代谢区以及各区间的通道和它们与系统外的联系(图1)。另一类把整个系统看成一个“暗盒”，不设定系统内的具体结构，只分析某物质在系统内总的运动规律，称非代谢区模型或随机模型。

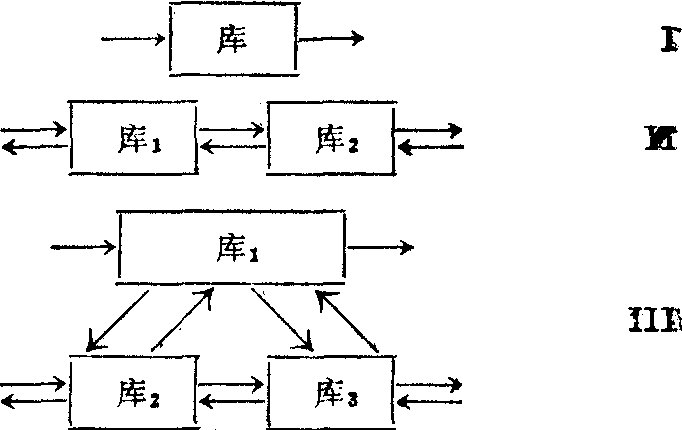
图1 示踪动力学几种常用的代谢区模型框图
不同系统的具体模型可能只具备部分通道
Ⅰ.单库模型 Ⅱ. 双库模型 Ⅲ. 三库模型

第二步是建立数学模型。针对设定的物理模型及预定引入示踪物的方法，建立一系列数学方程，以表达各动力学参数在理论上应有的相互关系。代谢区数学模型除表达各代谢区中示踪物的时相变化规律外，还给出各区的相互关系。非代谢区数学模型只给出示踪物在系统中总的时相变化规律及相应的动力学参数。
第三步是进行动物或人体实验。针对不同实验目的，示踪物可单次快速引入，也可恒速连续引入。少数实验采用其他途径引入示踪物，或多次重复引入示踪物。还有些实验应用两种或三种示踪物。直接引入示踪物的代谢区称初始区、初始库、或中室。间接得到示踪物的代谢区称次级区、次级库、或外室。引入示踪物后，根据所设数学模型的需要从初始库或（及）次级库采样，以求得示踪物在系统中或各代谢区中的时相变化数据。
第四步是对实验结果与设定的数学模型进行比较。通常是将实验数据用最小二乘法作多指数曲线拟合，找出一个能代表实验曲线的数学表达式。如果该表达式与原设定的数学模型相符合，则说明该模型能正确代表所研究的系统，于是便可将实验数据代入数学模型的各公式，求出一系列动力学参数。如果实验曲线的数学表达式与数学模型不符，则应提出新的理论假设，修改数学模型，直至两者相符为止。
医学上有时也对已知数学模型的系统进行实验，求出某些动力学参数以探讨他们在疾病状态下的变化情况。对这类实验，可直接将实验数据代入数学模型的有关公式求出动力学参数，通常不必再进行曲线拟合和比较。稳态和非稳态 正常成年人体内很多物质处于动态平衡，不论从整个系统或各个代谢区来看，输入速率和输出速率稳定，库大小不变，这种状态称为稳态。疾病时或某些生理性变化（如生长发育或怀孕）时，速率、速率常数及库大小等可能发生变化。如果这些变化在进行实验时已达到一个新的动态平衡，亦即在实验过程中不再发生变化，则仍属稳态。反之，如果在实验过程中，库大小或某些动力学参数仍在不断变化，亦即并未达到新的动态平衡，则属于非稳态。非稳态的数学模型与稳态的不同，计算更为复杂，故实验应当尽可能在稳态下进行。而对于非稳态系统，则需设计专门的数学模型，把非稳态因素包括在内。
稳态系统几种常用示踪动力学方法的原理 如下述：(1)一次引入示踪物后的代谢区分析： 大多数物质在代谢区中的消失属一级反应。示踪物一次快速引入单库系统后，库中物质的比放射性将按指数规律下降，其数学表达式为：

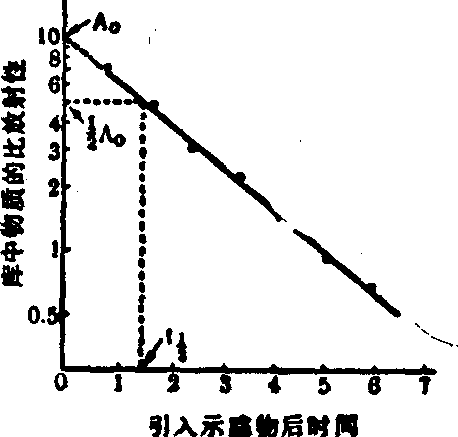
式中A₀是初始比放射性，A_t是经时间t后的比放射性，α为更新速率常数，t¹₂为半更新时间。实际工作中只需在半对数坐标上绘制实验所得的比放射性衰减曲线（应为直线），用直线回归法求出与纵坐标的相交点A₀及相应于₁^/2A₀的时间，即t_1/2，并按稀释法原理求出库大小，即可得到所需的各动力学参数(图2)。

双库系统中库之间若只有单向通道，可视为两个单库系统来处理。如果库之间有双向通道，则一次快速引入示踪物后，初始库的比放射性开始时下降特别迅速，在半对数坐标上呈很陡的曲线，待两库的比放射性达到平衡后转为直线。次级库的比放射性则先从零上升，到达一高峰值后转为下降

图2 稳态单库系统一次引入示踪物后的比放射性时相曲线

直线。曲线分解法可将初始库和次级库的曲线分别分解为两条直线。理论推导和实验都证明，两个库的两条相应直线分别有相等的斜率(图3)。
两库的比放射性时相曲线分别是两条直线之和，它们的数学表达式是：

式中A和B分别代表初始库及次级库的比放射性。对四条直线作直线回归即可求得A₀₁、A₀₁、B、α₁、α₂。初始库的初始比放射性等于A₀₁+A₀₂，用稀释法原理可算出初始库的库大小。次级库的库大小则需求出一系列动力学参数才能计算。

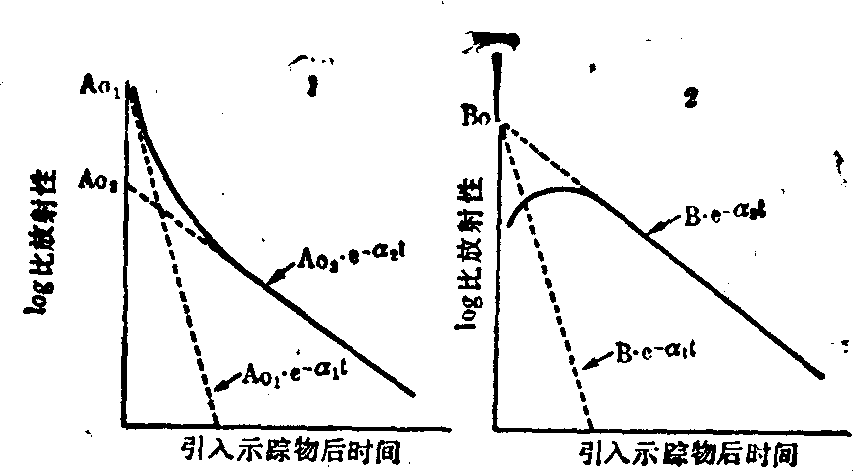
图3 具有双向通道的双库系统一次引入示踪物后的
比放射性时相曲线及其曲线分解
1. 初始库 2. 次级库 曲线分解是将实验曲线的直
线部分反向延长至与纵坐标相交，从实验曲线上各点
减去外推线上各相应值，得到另一条直线

进一步的工作是通过A₀₁、A₀₂、α₁、α₂等求出各通道的速率常数。按照各库的输入输出途径可列出各库放射性变化的微分方程，结合上述比放射性时相曲线的数学表达式，推导出求解速率常数的联立方程。求得速率常数后再按照其他动力学参数与速率常数、库大小及库中物质含量等的关系，计算出其他动力学参数。临床实践往往只能从初始库（血）采样，此时能求得多少参数将取决于具体系统实际存在的通道有多少。一般说，初始库和次级库的更新速率常数和更新时间、初始库的更新速率、清除率、排除速率、产生速率都可求出。
三库系统的曲线分解可得到三条直线，多库系统依此类推。它们的代谢区分析更为复杂，但原理及步骤与双库系统基本一致。
(2)一次引入示踪物后的非代谢区分析： 非代谢区分析即随机分析。本法不具体分析各库通道，而直接求出系统中某代谢库（通常是初始库）的某些动力学参数。第一步通常是在求出比放射性时相曲线的表达式后先计算库中某物质的排除速率DR。若任一瞬间库中的比放射性为At，则当时排除的放射性为At与DR的乘积。于是排除的全部放射性可用积分法求出。而排除的全部放射性应等于输入的总放射性，由此导出：

在此基础上，根据排除速率与其他参数的关系及不同模型的具体情况，可进而求出其他一些动力学参数。
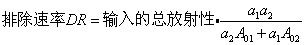
(3)恒速连续引入示踪物的非代谢区分析： 这种方法的原理是： 初始库中物质的比放射性先从零逐渐升高，随后达到一稳定值，称为坪值。坪值的到达意味着输入标记物的速度与输入非标记物的速度保持一定的比例，而该比例正好等于比放射性的坪值，亦即标记物输入速度为已知值，比放射性坪值可由实验求得，故物质的输入速率（稳态时等于更新速率）可由此算出。进一步求其他动力学参数的简便方法是停止输入标记物后测定库中物质的比放射性时相曲线。该曲线应与一次引入示踪物后的时相曲线后段相似，呈一下降的指数曲线。t及更新速率常数可直接从指数曲线求出， 库大小则等于更新速率常数除更新速率。