直言三段论

即“三段论”。

直言三段论

由直言命题所组成的一种推理形式，简称三段论。传统逻辑的三段论演绎体系是由亚里士多德创立的，在中世纪得以完善，现代的数理逻辑对三段论也作过专门的研究。
三段论的结构 一个直言三段论由三个直言命题所组成，其中两个为前提，一个为结论。三个直言命题包含三个相同的词项，其中只在两个前提中出现而不在结论中出现的词项称为中项，用字母“M”表示；在结论中作为主词的词项称为小项，用字母“S”表示；在结论中作为宾词的词项称为大项，用字母“p”表示。两个前提中包含大项的前提称为大前提，包含小项的前题称为小前提。在排列顺序上，通常大前提在前，其后是小前提，最后为结论。但这种顺序不是绝对的。
三段论的公理 又称曲全公理。直言三段论推理的依据。内容为：凡对一类事物有所肯定，则对该类事物中的每一个对象也有所肯定；凡对一类事物有所否定，则对该类事物中的每一个对象也有所否定。可用下面两图表示三段论的公理：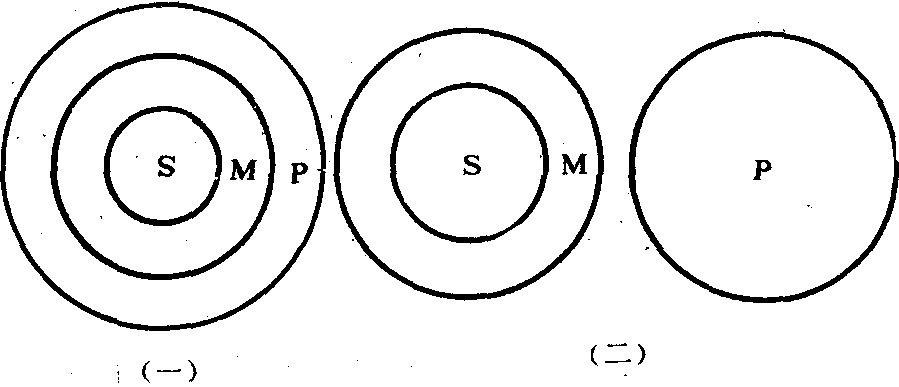

图(1)表示，对一类事物M肯定其具有属性P，那么M类中部分对象S也必然具有属性P。图(2)表示，对一类事物M否定其具有属性P，那么M类中部分对象S也必然不具有属性P。
三段论的规则 要保证直言三段论推理的有效性，就必须遵守一定的规则。三段论的规则共二类四条。第一类是关于词项的规则：（一）在前提中，中项至少要周延一次；（二）词项只有在前提中周延，才可在有效的结论中周延。第二类是关于质的规则：（一）至少有一个前提必须是肯定的；（二）如果有一个前提是否定的，则结论必须是否定的。从这四条基本规则出发可以证明一些从属的规则，例如，两个特称的前提推不出结论；如果前提中有一个是特称的，则结论必须是特称的；如果结论是肯定的，则两个前提必须是肯定的；如果结论是全称的，则两个前提必须是全称的；如果结论是否定的，则两个前提中必有一个是否定的。
三段论的格 直言三段论中由于中项在前提中的位置不同而构成的不同形式。三段论有四个格。第一格，中项是大前提的主词，小前提的宾词。第二格，中项在大小前提中都是宾词。第三格，中项在大小前提中都是主词。第四格，中项是大前提的宾词，小前提的主词。四个格的结构如下图：

根据三段论总的规则，结合各个格的具体形式，可以引申出每个格的具体规则。第一格：（一）大前提须是全称的；（二）小前提须是肯定的。第二格：（一）两个前提中须有一个是否定的；（二）大前提须是全称的。第三格：（一）小前提须是肯定的；（二）结论须是特称的。第四格：（一）如果大前提是肯定的，则小前提必须是全称的；（二）如果小前提是肯定的，则结论必须是特称的；（三）如果前提中有一个是否定的，则大前提必须是全称的。
三段论的式 直言三段论的大前提、小前题和结论都可能由A、E、I、O中的任一个命题充当，共有64种可能的组合；再考虑到三段论有四个格，所以就有256种可能的组合。每一种组合称为一个式。在256个式中，符合三段论规则的叫有效式，违反三段论规则的叫无效式。三段论的有效式共24个，分别如下：
第一格：AAA,EAE,AII,EIO,(AAI),(EAO);
第二格：AEE,EAE,EIO,AOO,(AEO),(EAO);
第三格：AAI,AII,EAO,EIO,IAI,OAO;
第四格：AAI,AEE,EAO,EIO,IAI,(AEO)。
上列各式中19个不带括号的叫强式，5个带括号的叫弱式。弱式本可以得出全称命题为结论，但只以特称命题为结论。中世纪经院逻辑为了便于记忆，分别给这19个强式以特殊的名称，并编成“格式歌诀”。例如，Barbara,Celarent分别表示第一个格的AAA式和EAE式。除了这24个有效式外，其余的232个式都是无效式。
三段论的化归 在传统逻辑中，直言三段论是一个近似完整的公理体系。其中，第一格的AAA式和EAE式起着公理的作用，其他17个强式的有效性须通过这两个式加以证明。证明的方法是用有效的逻辑方法把这17个式化归（又叫还原）为第一格的AAA式和EAE式。化归的方法有两种。一种是直接化归，将前提或结论换位，或将两前提对调，就可把其他格化归为第一格。例如，第三格的IAI式具有下面的形式：

把它的大前提换位，再把大小前提对调，最后把结论换位，即成为

这就是第一格的形式。另一种是间接化归，使用归谬法，把否定了的结论与一个否定了的前提对调，从而化归为第一格。例如，第二格的AOO式具有下面的形式：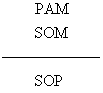

把结论SOP否定，得SAP；再把前提中的SOM否定，得SAM；然后把它们对调，即成为

这就是第一格的AAA式。所以使用这种方法，是因为前提中含有O命题，而O命题是不能换位的。
三段论的现代研究成果 用谓词逻辑的符号来表示三段论的推理式，则三段论的有效式都可从谓词逻辑系统中推出，其中9个从两个全称前提得出特称结论的式，须将主词存在这一传统逻辑隐含的前提揭示出来。这表明三段论推理只是谓词逻辑的一部分。卢卡西维茨(J·Lukasiewicz 1878—1956)用数理逻辑为工具，对三段论体系作了专门研究。他用a,b,c等表示词项，用A、I代表算子，采用前置号的方法，Aab表示“所有a是b”，Iab表示“有的a是b”。将Eab(所有a不是b)定义为Iab的否定，Oab(有的a不是b)定义为Aab的否定。用下面四条公理：
（一） Aaa
（二） Iaa
（三） Abc ∧ Aab→Aac
（四） Abc∧Iba→Iac
其中第三条公理是三段论第一格的AAA式，第四条公理是第三格的AII式。再借助代入规则、分离规则以及命题演算的规律，就可推出直言命题的换位规律和所有的三段论的有效式。这个完全形式化的三段论公理系统的建立使人们对传统逻辑的三段论体系有了新的认识。