直角三角形的判定定理zhijiao sanjiaoxing de pan dingdingli

❶若一个三角形一边上的中线等于这边的一半，则这个三角形是直角三角形.
如图1,BD是AC边上的中线，且BD=AC/2，则∠ABC=90°;

❷若一个三角形的一条边的平方等于其他两边的平方和，则这条边对的角为直角，这个三角形是直角三角形.如图2,AC²＝AB²+BC²,△ABC是直角三角形（勾股定理逆定理）.

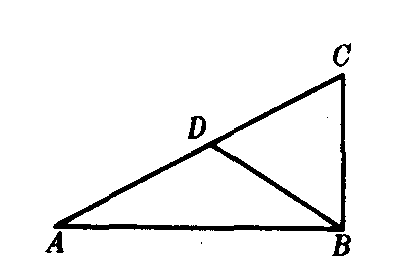
图1

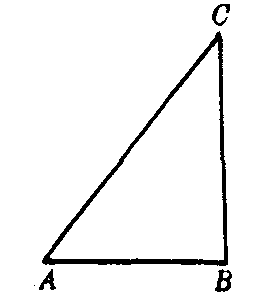
图2

这个定理在欧几里得的《原本》中是这样证明的.如图2，在△ABC中，AC²＝AB²+BC².证明∠ABC=90°.
证明：作BD⊥BC，且BD=AB，连结DC.由AC²＝AB²+BC²,CD²＝BD²+BC²（勾股定理），所以AC²＝CD²，即AC=CD.故△ABC≌△DBC.因此，∠ABC=∠DBC=90°.