直线回归linear regression

指两种现象或事物的数量变化存在着互相依存的因果关系。由一种变量(自变量x)的变化，根据直线回归关系的函数方程，计算出另一种变量(因变量y)的变化，即由一种变量的实际值计算出另一种变量的估计值。

直线回归

直线回归是处理两变量（其中至少有一个是随机变量）间线性依存关系的一种统计分析方法。如人的体重与体表面积之间存在着一定的关系，其散点图呈一直线趋势，(见图1)。根据各对观察值可求得一直线方程，以说明两变量间依存变化的数量关系。但图中各观察点并不完全在一直线上，与数学上完全确定的函数图象不同，这种直线方程具有某种不确定性，称为直线回归方程。
“回归”一词创用于F. Galton (1887)，他从表达父子身高的一些直线方程中发现父高子亦高，但一群高（或矮）个子父亲的儿子们，平均身高却低（或高）于父亲们的平均身高，向男子身高的总体均数“回归”，于是后来将表示这类变量间关系的方程称回归方程。
用途：
❶两变量间存在直线关系时，求出直线方程来描述这种关系；
❷根据直线回归方程由已知（或易测）变量值，估计未知（或难测）变量值；
❸对总体回归直线作出估计，说明样本回归直线的可信程度；
❹估计正常值范围，如对不同体重者估计其体表面积的正常值范围；
❺为协方差分析的基础等。直线方程的通式为

式中X为自变量， Ŷ为应变量Y的估计值亦称回归值。a为直线在Y轴上的截距，即X=0时的Ŷ值。 b为直线的斜率，称回归系数，表示X变动一个单位时，Ŷ平均变动的单位数。求直线方程就是计算方程中a和b的值，常用最小二乘法原理。
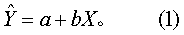
根据最小二乘法原理，式(1)中b和a可按式(2)和式(3)求得，此时估计误差平方和∑(Y-Ŷ)²最小。

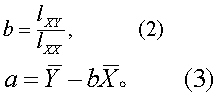
式(2)中lXX为X的离均差平方和，lXY为离均差积和，算法如下：

lXX=∑(X-)²＝∑X²-(∑X)²/n,
lXY=∑(X-)(Y-)=∑XY-(∑X)(∑Y)/n,

式中n为样本含量。
若要求直线过定点(X₀,Y₀)，则

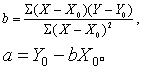
若要求直线过(0,0)点，则

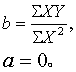
当观察点的直线趋势很明显时，亦可用目测法等求直线回归方程。
用最小二乘法计算直线方程的步骤：
(1)将n对观察值在直角坐标纸上绘散点图，如果散点呈直线趋势，再进行下列步骤。
(2)计算∑X,∑X2,∑Y,∑XY。
(3) 求, ,lXX, lXY。
(4)按式(2)与式(3)求b、a得直线方程。
(5) 画直线。取相距较远的两X值，分别代入方程求出相应的Ŷ值，得两点坐标，过此两点的直线即回归直线。
例1 测得某地3岁儿童10人的体重与体表面积见表1，试求由体重推算体表面积的回归方程。

表1 某地三岁儿童10人的体重与体表面积

体 重， X (kg)	体表面积，Y (103cm2)
11.0 11.8 12.0 12.3 13.1 13.7 14.4 14.9 15.2 16.0	5.283 5.299 5.358 5.292 5.602 6.014 5.830 6.102 6.075 6.411

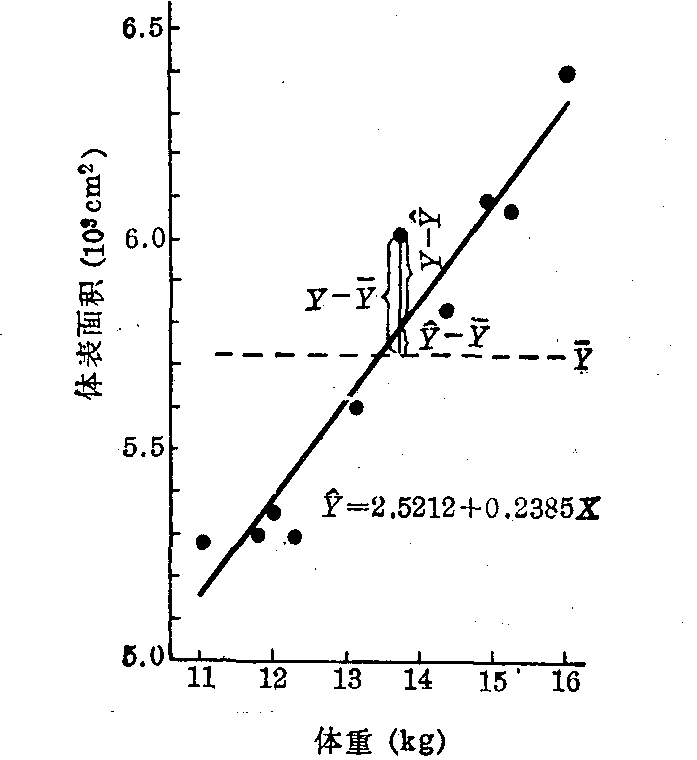
图1 某地3岁儿童体重推算体表面积的直线回归方程散点呈直线趋势(见图1)。

过点(11,5.145)与(15,6.099)作直线见图1。
直线回归方程的假设检验 亦即回归系数的假设检验。观察值Y₁,Y₂，…，Y_n之间的变异由两方面的原因引起：自变量X的变化和其他因素如实验误差等的影响。为了检验哪方面的影响是主要的，先将Y变异的总离均差平方和SS_总(即l_YY)分解为两部分(见图1示意):

<称为回归平方和。SS回/自由度为回归方面的均方，它是由X的变化所引起的，在直线回归中自由度为1。

称为剩余平方和。SS剩/自由度为剩余均方，表示观察点与直线的偏离（纵向距离），它是由实验误差以及其他未加控制的因素所引起的，自由度为n-2。
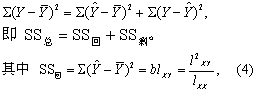
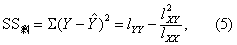
如果Y与X之间无直线关系，那么样本所来自的总体的回归均方与剩余均方应相等，或回归系数β=0；反之，β≠0。所以要检验Y与X之间是否有直线关系，可用F检验或t检验。检验假设H₀为β=0，检验结果若不拒绝H₀，不能认为X与Y之间有直线关系；若拒绝H₀，则可认为有直线关系，只有这时才能求直线回归方程。检验步骤：
(1) 求∑X,∑Y,∑X₂,∑Y₂,∑XY;
(2) 求lXX,lYY,lXY;
(3)若用F检验，则按式(6)计算统计量F值。

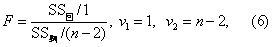
式中SS回按式(4)计算，SS剩按式(5)计算，求得F值后，查F界值表得P值，按所取检验水准作出推断结论。
若用t检验，则按式(7)计算统计量t值。

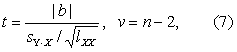
式中b按式(2)计算：分母为回归系数的标准误s_b，其中sY·X为剩余标准差，即剩余均方的平方根，按式(8)计算。

式中∑(Y-Ŷ)²由式(5)求得。 求得t值后，查t界值表得P值，按所取检验水准作出推断结论。
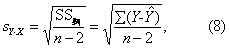
对同一资料，这两种检验所得的结论是一致的，因为在v1=1时，_t＝。
例2 对例1的直线回归方程（或回归系数）作假设检验。
H₀: β=0,
H₁: β≠0。
α=0.05。
由例1得∑X=134.40,∑Y=57.266,
∑X₂＝1831.24,∑Y₂ = 329.4834,∑XY=775.5946;l_XX＝24.9040,l_XY＝5.9396。

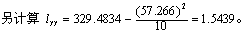
(1) F检验。由式(4)～(6)

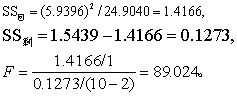
今v₁＝1,v₂＝10-2=8，查F界值表，得P<0.01。按α=0.05水准拒绝H₀，接受H₁，可认为两变量间有直线关系，可以求直线回归。
(2) t检验。前已求得SS剩=0.1273 ,b=0.2385,lxx=24.9040，代入式(8)及式(7):

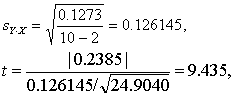
v=10-2=8。查t界值表得P<0.01，按α=0.05水准拒绝H₀，接受H₁。结论同F检验。这里t=, 即9.435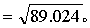
作直线回归分析时应注意：
(1)两变量间的关系必须有实际意义。
(2)计算直线回归的两变量，若X为选定的，则对应于每个X值的Y值须服从正态分布，其Y即Y的均数；若X、Y都是随机变量，则要求X、Y服从双变量正态分布。否则须先经变量变换，使资料符合要求后再进行回归分析。
(3)用同一资料计算由X推算Y (b₁＝l_XY/l_XX,α1=-b₁)和由Y推算X (b₂＝l_XY/l_YY, a₂＝-b₂)的两个直线回归方程，结果不同。因此要正确选定自变量。若两变量间有因果关系，应以“因”为X；无因果关系，则以较易测定者或变异较小者为X，否则可能加大误差。
(4)观察值必须是同质的。如果有两个不同的子群，可能产生实际上不存在的回归[图2(a)]，也可能忽视了确实存在的回归关系[图2(b)]。

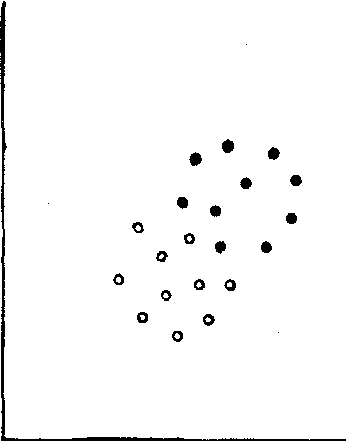
(a) 误为有回归

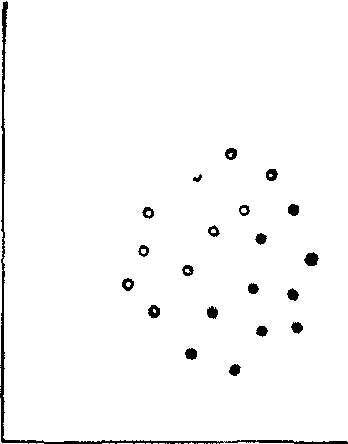
(b) 回归被忽视

图2 存在两个子群对回归的影响

(5) 回归方程一般只适用于自变量X的原观察数据范围，而且实验条件也应与取得原观察数据时的实验条件一致。
(6)直线回归的数学模型为

Y=a^*+βX+ε,

式中a^*为总体回归直线在Y轴上的截距，β为总体回归系数，ε为观察点(X,Y)与直线的偏离（纵向距离），是由实验过程中一些随机因素造成的误差。应用最小二乘法的条件是假定误差ε独立，且各X值处ε的方差相等，若违反此假定则不适用：如(1)Y值在时间（或空间）上接近者比相距较远者更相似，即Y值存在自相关；或(2)散点(X,Y)呈扇形分布，即X增大时Y的方差亦增大。