百鸡问题

048 百鸡问题

世界著名的数学问题之一。载于《张丘建算经》卷下之末，为全书压卷之题。原题为：“今有鸡翁一，直(值)钱五；鸡母一，直钱三；鸡雏三，直钱一。凡百钱，买鸡百只。问鸡翁、母、雏各几何？”这是一个不定方程组问题。
设鸡翁、母、雏各为x、y、z只，则

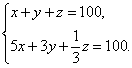
其整数解为(4t,25—7t,75+3t). 因x、y、z均为非负整数，故取t=0,1,2,3，本题有以下四组解： (0,25,75)、(4,18,78)、(8,11,81)、(12,4,84). 《张丘建算经》给出了其中后三组正整数解。但未给出具体解法。只有三句术文：鸡翁每增四，鸡母每减七，鸡雏每益三，即得。”百鸡问题为后世数学家所重视，曾有多人进一步加以研究。清代丁取忠在《数学拾遗》中先假设无鸡翁，求出鸡母数25、鸡雏数75，此时3y+1/3z=100，为使鸡数不变，z每增3,y必减3，则钱少8。而1只鸡翁比1只鸡母多钱2，为使钱数不变，只须将4只鸡母换成4只鸡翁。从而使“增四”、“减七”、“益三”之理得到解释。其后，时曰醇推广百鸡题，撰《百鸡术衍》，使这个古老问题灿然大著。“百鸡术”即中国古代求解一次不定方程组的方法，在世界上流传颇广。印度的摩诃毗罗(9世纪)和婆什迦罗第二(12世纪)、埃及的阿布·卡米尔(9世纪)、意大利的L. 斐波那契(13世纪)和列奥那多(13世纪)及阿拉伯的卡西(15世纪)的著作中均有类似问题。可见“百鸡术”是中外数学交流的一个重要线索，在中世纪世界数学史上有着特殊的意义。

百鸡问题Baiji wenti

《九章算术》方程章有一个 “五家共井”问题， 原文如下：
“今有五家共井， 甲二绠(绠：汲水用的绳子)不足，如乙一绠(注：井深比二条甲家绳长还多一条乙家绳长); 乙三绠不足，如丙一绠；丙四绠不足，如丁一绠；丁五绠不足，如戊一绠；戊六绠不足，如甲一绠。如各得所不足一绠。皆逮(逮：到达)。问井深、绠长各几何。”
设甲、乙、丙、丁、戊家一绠之长分别为x,y,z,u,v，井深为W，根据题意可列出方程组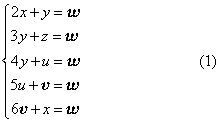
由于题中有6个未知数，却只能列出5个独立的方程，因此是一个不定方程组问题，又由于其中每个方程都是一次齐次式，解法很容易，只需求出其中5个未知数关于第6个未知数的比率， 于是给出第6个未知数的一个值，就对应了整个不定方程组的一组解，其解显然有无穷多组，《九章算术》中仅给出了一组解：w=721,x=265, y=191, z=148, u=129, v=76, 公元3世纪，刘徽在给《九章算术》作注释时指，原书只是给出了未知数之间的比率， 从而正确地认识了这个问题的性质。
由于“五家共井”问题过于简单，还不能代表一次不定方程组求解中的特点与困难。最早表现出中国古代数学家在一次不定方程组方面成就的，是5世纪《张丘建算经》(参见 “算经十书”) 中的 “百鸡问题”：
“今有鸡翁（大公鸡）一值钱五，鸡母一值钱三，鸡雏三值钱一。凡百钱买鸡百只，问鸡翁、母、雏各几何。”
若设鸡翁、母、雏的只数分别为x,y,z，根据题意可得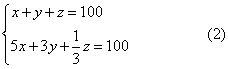
书中给出了全部正整数答案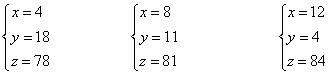
并且提出：“鸡翁每增四，鸡母每减七，鸡雏每益三，即得。”这实际上指出，在求得了方程组(2)的一组特解(x₀,y₀,z₀) 之后， 其余的解可由下列关系得到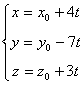
其中t取适当的整数值， 使所得结果符合题意。
“百鸡问题”在中国和世界数学史上影响十分深远。在中国，南北朝时北周数学家甄鸾在《数术记遗》(参见“算经十书”)中列举了两道百鸡问题： “今有鸡翁一只值五文，鸡母一只值四文，鸡儿一文得四只。今有钱一百文，买鸡大小一百只，问各几何。”“今有鸡翁一只值四文，鸡母一只值三文，鸡儿三只值一文。今有钱一百文，还买鸡大小一百只，问各几何。”甄鸾分别给出一组特解 (15, 1, 84)和 (8, 14, 78)。南宋数学家杨辉在其《续古摘奇算法》(1275)中曾引用早已失传的《辩古根源》中的一题：“钱一百买温柑、绿桔、扁桔共一百枚。只云温柑一枚七文，绿桔一枚三文.扁桔三枚一文，问各买几何。”在清代，百鸡问题曾引起不少学者对一次不定方程组的广泛研究。
在其他各国也曾出现过许多与百鸡问题十分相似的问题，其中不乏受到中国数学影响的痕迹。8世纪英国学者阿尔昆 (Alcuin) 在其 《益智题》一书中载有：“一百袋谷分给一百个人，男人一人三袋，女人一人二袋， 小孩二人一袋。问男人、女人、小孩各几人。”书中只给出一组解(11, 15,74)。在印度9世纪数学家摩诃毗罗(Mahavira)、12世纪数学家婆什迦罗（参见该条）的著作中均有算题： “鸽子3卢比5只，寒拉鸟5卢比7只， 孔雀9卢比3只， 鹅7卢比9只。今100卢比买100只鸟，问各种鸟可买几只。”13世纪，意大利数学家斐波那契在他的著作中给出： “某人花30文钱买了30只鸟，其中麻雀三只1文，雉鸡两只1文，鸽子每只两文。问每种鸟各几只。” 1427年，阿拉伯数学家阿尔 ·卡西(al-Kashi)在他的 《算术之钥》中也给出了这样的问题： “鸭一值四钱，雀四值一钱，鸡一值一钱，凡百钱买百鸟，问鸭、雀、鸡各多少。”可以说，百鸡问题既是古代一次不定方程组研究的重要内容，又是中外数学交流的一条重要线索， 在世界数学史上有着特殊的意义。