电荷量子化dianhe liangzihua
电荷不以连续方式存在,而以分离的某一基元电荷存在。这个基元电荷就是一个电子所带的电量,叫电子电荷,用e表示。其值为1.60210×10-19库仑。在物理上任何存在着的电荷q,不问其来源如何,都可以写成ne,n是正的或负的整数。
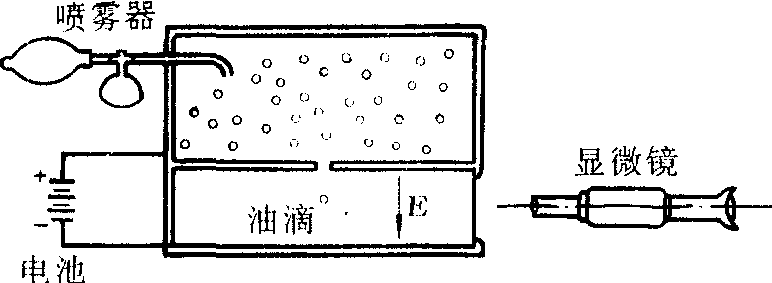
富兰克林时代,电荷被设想成连续的流体。直至1911年R.A.密立根通过油滴实验测得所有油滴所带电荷都是基元电荷e的整数倍,而得出电荷量子化的概念。密立根油滴实验装置如下图所示,一个很小的带电油滴在电场E内,调节E,使作用在油滴上的电场力与油滴的重量平衡从而测得该油滴电荷。然后换一个带电油滴再进行测量。由已知油的密度,例如为0.851克/厘米3,测得油滴的半径,密立根测量油滴半径的方法是,撤去电场,由观测油滴在空气中降落的极限速度去计算得到,例如为1.64×10-4厘米,就可得知油滴的质量和重量。测得平衡时的场强E=1.92×105牛/库仑,可计算出油滴电荷为8.204×10-19库仑。密立根是用一阵阵x射线照射油滴而使油滴带电的。早期密立根在一连串实验中所测得的不同单个油滴上呈现的电荷如下:
6.563×10-19库仑 18.08×10-19库仑8.204×10-19库仑 19.71×10-19库仑11.50×10-19库仑 22.89×10-19库仑13.13×10-19库仑 26.13×10-19库仑16.48×10-19库仑
若考虑测量误差,密立根所得基元电荷为1.64×10-19库仑,与现在所使用的数值1.602×10-19有一定的偏离,但它表明,所有电荷电量为一基元电荷的整数倍。密立根的具体实验和计算方法是:当电场力与重力平
不能直接测量。在无电场时,油滴在重力作用下下落,当重力与粘滞系数为η的流体粘滞力平衡时,小滴将匀速下落。斯托克斯定律给出f=6πηγv,又f=mg,所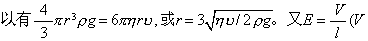 为电位差,l为板距),最后有
为电位差,l为板距),最后有
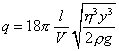
严格讲,这公式还应有所修改,例如ρ应该用(ρ -ρ0)去代替,ρ0为空气密度。其次空气也不是连续流体。
- 尼麦角林是什么意思
- 尼麦角林是什么意思
- 尼龙1010接头是什么意思
- 尼龙11管材的生产是什么意思
- 尼龙66座是什么意思
- 尼龙地毯是什么意思
- 尼龙的密度是什么意思
- 尼龙-6是什么意思
- 尼龙-610是什么意思
- 尼龙-66是什么意思
- 尽快排泄体内已经吸收的毒物是什么意思
- 尽职调查是什么意思
- 尾骨挫伤与尾骨痛是什么意思
- 尾骨骨折与脱位是什么意思
- 尿17-生酮类固醇测定是什么意思
- 尿17-羟皮质类固醇测定是什么意思
- 尿17-酮类固醇测定是什么意思
- 尿便障碍的诊断与治疗是什么意思
- 尿促性素是什么意思
- 尿促性素是什么意思
- 尿促性素是什么意思
- 尿促性素是什么意思
- 尿及粪汁中全氮测定(硫酸消煮-甲醛容量法)是什么意思
- 尿嘧啶氮芥是什么意思
- 尿囊素是什么意思
- 尿囊素是什么意思
- 尿失禁是什么意思
- 尿失禁是什么意思
- 尿失禁是什么意思
- 尿失禁是什么意思
- 尿崩症是什么意思
- 尿崩症是什么意思
- 尿崩症是什么意思
- 尿崩症是什么意思
- 尿崩症是什么意思
- 尿崩症是什么意思
- 尿布和卫生餐巾用表面吸附材料是什么意思
- 尿布洗涤剂是什么意思
- 尿布皮炎是什么意思
- 尿布皮炎是什么意思
- 尿布皮炎是什么意思
- 尿布胶(油包水型乳胶)是什么意思
- 尿毒症是什么意思
- 尿浓缩与稀释的原理是什么意思
- 尿浓缩与稀释的概念是什么意思
- 尿液免疫学检查是什么意思
- 尿液免疫学检验是什么意思
- 尿液检查是什么意思
- 尿液检查是什么意思
- 尿液检查是什么意思
- 尿液检查项目及其数值是什么意思
- 尿液检验是什么意思
- 尿液生化检查是什么意思
- 尿液生化试验是什么意思
- 尿潴留是什么意思
- 尿潴留是什么意思
- 尿潴留是什么意思
- 尿激酶是什么意思
- 尿激酶是什么意思
- 尿激酶是什么意思