电场强度的叠加原理dianchang qiangdu de diejiayuanli

经典电磁学的一条基本原理。其内容为：几个点电荷所激发的电场在某点的（总）场强等于各个点电荷单独存在时所激发的电场在该点的场强的矢量和。电场强度的迭加原理简称场强迭加原理。在静电场中，场强的迭加原理可由库仑力的迭加原理导出。库仑力的迭加原理是一个实验事实，当空间有两个以上的点电荷时，作用于每一个点电荷上的总静电力等于其它点电荷单独存在时作用于该点电荷的静电力的矢量和。如果空间有三个点电荷q₁、q₂和q₃，对于其中任一个，例如对于q₃的作用力F₃，根据这一原理可表达为

r13、r23分别为q₁、q₂指向q₃的单位矢，r₁₃、r₂₃分别为q₁、q₂与q₃之间的距离，这意味着，一个点电荷作用于另一点电荷的静电力总是符合库仑定律，与其周围是否存在其它电荷无关。由上式，根据场强定义，并将q₃理解为试探电荷q0，则该处的场强为
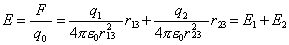
E₁、E₂为q₁、q₂单独存在时在该点的场强。对n个点电荷产生的场、观察点（场点）的场强为

根据场强的迭加原理，可以求点电荷系的场强，这时根据点电荷的场强公式与迭加原理有

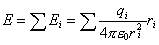
r_i和r_i分别为q_i到场点的距离和指向场点的单位矢。例如由此式可求得电偶极子所产生的场强。对于连续分布的带电体的场强，也可由迭加原理求出。方法是将带电体看成许多物理无限小体元的组合。每一无限小体元对场点而言均可看成点电荷，总场强就是这些点电荷的场强的矢量和，即

在极限情形下，上式变为矢量积分

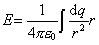
在更一般的情况下，空间除了库仑电场E库之外，还存在感生电场（或涡旋电场）E涡。大量实验事实证明，这时场强的迭加原理仍然存在。即场中一点的场强为

E=E库+E涡

也就是说总场强等于库仑电场与涡旋电场的矢量和。

电场强度的叠加原理

电磁学中一个表示电场基本性质的原理。它表述为：电场中任一点的总场强等于各个点电荷单独存在时在该点各自产生的场强的矢量和。