田中法
田中法
亦称“最合适区域法”。价值 工程中通过计算价值系数,选择价值工程对象的方法。由日本田中教授在1973年提出。其思路是: 价值系数相同的对象,由于各自的成本系数与功能评价系数的绝对值不同而对产品价值的实际影响有很大差异。因此,在选择对象时,不应把价值系数相同的对象同等看待,而应优先选择对产品实际影响大的对象。应用这种方法的关键是确定最合适区域,其作法是: 以成本系数为横坐标,以功能评价系数为纵坐标,绘制价值系数坐标图,则与X轴、Y轴成45°夹角的直线即为价值系数V=1的标准线。最合适区域由两条围绕标准线V=1的曲线包络而成 (右图中斜线所示区域)。凡落在区域内的对象,都被认为其价值系数对于V=1的偏差是允许的,因此不列为价值工程对象,而在区域外的点,特别是距离区域远的,则应优先选为价值工程对象。构成最合适区域的这两条曲线的方程为: 当xi>yi时,; 当xi 最合适区域图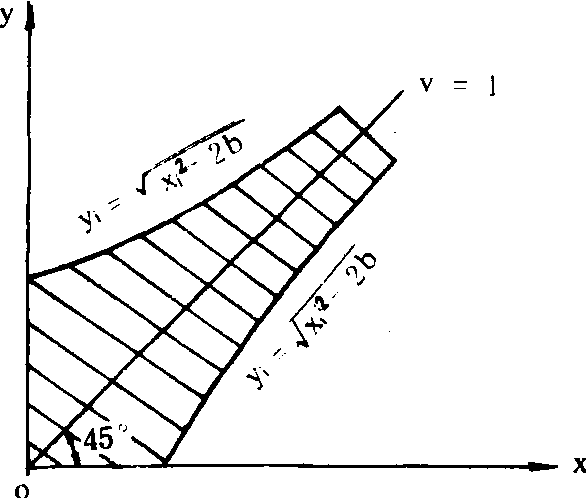
☚ 价值系数 方案组合法 ☛
- 屋笆开门是什么意思
- 屋簷是什么意思
- 屋粟是什么意思
- 屋翳是什么意思
- 屋翼是什么意思
- 屋肐拉子是什么意思
- 屋肚肠是什么意思
- 屋肚里是什么意思
- 屋背是什么意思
- 屋背头是什么意思
- 屋脊是什么意思
- 屋脊上放西瓜是什么意思
- 屋脊上睡觉——不知往哪边翻身是什么意思
- 屋脊上睡觉——翻不过身来是什么意思
- 屋脊上贴告示是什么意思
- 屋脊子是什么意思
- 屋脊梁是什么意思
- 屋舍是什么意思
- 屋舍俨然是什么意思
- 屋舟是什么意思
- 屋茨茅,蹊种竹,畹滋兰。是什么意思
- 屋荣蔡是什么意思
- 屋荫是什么意思
- 屋落是什么意思
- 屋落尘是什么意思
- 屋蓋是什么意思
- 屋蘭是什么意思
- 屋蜡灰是什么意思
- 屋蠧是什么意思
- 屋要人支,人要粮撑是什么意思
- 屋角头是什么意思
- 屋角尽悬牛蒡草,篱根多发马兰花。是什么意思
- 屋角愿是什么意思
- 屋角暂辞千树雪,马头犹带一枝春。是什么意思
- 屋角的充分利用是什么意思
- 屋角的檐部向上翘起的建筑形式是什么意思
- 屋角菜花黄映篱,桥边柳色绿摇丝。是什么意思
- 屋誅是什么意思
- 屋诛是什么意思
- 屋课是什么意思
- 屋质定变是什么意思
- 屋质定计息干戈是什么意思
- 屋贮娇是什么意思
- 屋辚是什么意思
- 屋边是什么意思
- 屋边大树砍伐祭仪是什么意思
- 屋透水是什么意思
- 屋都水是什么意思
- 屋里是什么意思
- 屋里不烧火,屋外不冒烟是什么意思
- 屋里不见路上见是什么意思
- 屋里个是什么意思
- 屋里人是什么意思
- 屋里佬是什么意思
- 屋里使唤是什么意思
- 屋里厢是什么意思
- 屋里向是什么意思
- 屋里头是什么意思
- 屋里头的是什么意思
- 屋里家是什么意思