生命表life table

在一个同龄个体群中，任一个体有可能存活到年龄为x的概率的一览表。即将一特定种群的死亡数量、死亡原因，死亡年龄等资料列成表，以便从中分析该种群生活史过程中引起数量变化的原因。这是昆虫种群动态研究最有效的手段之一。
简史 生命表最先是英国格朗特 (J.Graunt)1662年设想的，以后被应用于人类保险方面的研究。珀尔(R.Pearl)1921年首先用于果蝇实验种群的研究，1941年又研究了杂拟谷盗实验种群。加拿大莫里斯和米勒(R. F. Morris & C. A. Miller,)1954年最先研究了云杉卷叶蛾自然种群生命表。此后，生命表技术被广泛用于各类害虫种群动态研究，在害虫综合治理中用于预测预报和评价各种防治措施的效果，为制定正确的防治策略和措施提供理论基础。
分类 生命表有以下3种类型：特定时间生命表(time-specific life table)、特定年龄生命表 (age-specific life table)和世代平均生命表(generation-mean life table)。分别适用于世代重叠、离散和不完全重叠的情况。
特定时间生命表 适用于具有稳定年龄组配和世代完全重叠的昆虫种群的研究。这种生命表假设昆虫种群是静止而世代重叠的、不同年龄级的个体在出生时数目相等。在特定时间对种群随机抽样，检查各年龄级的个体数，其个体数差异就是年龄间的死亡数，以此推算年龄间的死亡率和平均生命期望。表1为假设的特定时间生命表。

表1 假设的特定时间生命表

x	lx	lglx	dx	1000qx	ex	Lx	Tx
1 2 3 4 5	1 000 450 200 50 10	3.0 2.7 2.3 1.7 1.0	550 250 150 40 10	550 556 750 800 1.000	1.21 1.08 0.80 0.70 0.50	725 325 125 30 5	1 210 485 160 35 5

表中 x为年龄间隔或年龄级；l_x为年龄间隔x开始时存活的个体数，即l_x+1＝l_x—d_x; d_x为年龄间隔x到x+1的死亡数； q_x为年龄间隔x到x+1的死亡率，即1000 q_x＝d_x/l_x×1000; L_x为年龄间隔x到x+1生存个体平均数，也称生命表年龄结构，即L_x＝l_x+l_x+1/2:T_x为L_x栏从底层往上叠加的共计数，以个体×时间为单位， 即T_x＝L_x; e_x为在年龄开始时存活的个体的平均生命期望值，即e_x＝T_x/l_x。生命表的上述形式，仅仅从死亡率考虑种群的变化，但引起昆虫种群变化除死亡率外还要考虑出生率，把种群的出生率引入生命表中，在上述生命表的基础上构成了种群的生殖力表(表2)，这是特定时间生命表的另一种形式。

表 2 小褐金龟甲出生率表
(录自R. Laughlin)

表2中的x、lx与表1相同，但l_x仅代表存活的雌虫数。mx表示每个年龄间隔每雌产下的活雌虫数，又称特定年龄生育力(age-specific fertility)。在实践中常假设性比为50:50,m_x＝N_x/2,N_x为年龄x的雌虫每雌总出生数，种群的增长既决定于存活的雌虫数，亦决定于每雌所产生的后代数，即决定于l_x与m_x的乘积，l_x·m_x(=V_x) 是年龄为x的雌虫产下的雌性子代数。净出生率 R₀＝∑lxm_x，表2中年龄级x的时间间隔为周，从0到54周，净出生率R0为2.94，即1个世代过程中，1个雌虫平均产下2.94个雌性子代_。如果R0＝1，种群处于稳定状态，R₀>1，种群数量增加，R₀<1，种群数量下降。已知R0，就可近似的计算出种群增长瞬时速率(r):

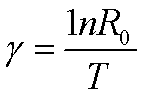
式中 平均世代时间(T)，可以下式计算出：

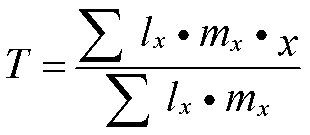
r作为比较不同种的种群增长率或同种群在不同的环境条件下的增长速率是很有用的。在最适宜的条件下，r可作为rm（种群内禀增长率）或rmax （种群最大增长率） 的等价值。对很多昆虫来说，世代是明显离散的，种群出生率和死亡率因受环境的影响而经常变动，种群数量也不断变动，所以利用特定时间生命表研究这类现象时有一定局限性。
特定年龄生命表 适用于世代离散的昆虫种群动态研究。通常取一定数量出生期基本一致的个体 （同龄个体群），观察记载进入生活史各虫态的个体数、死亡数、死亡原因(表3)。注重的不是个体的生命期望，而是特定年龄组中的死亡原因。通过对各种死亡因素进行定量，可以分析引起种群数量变动的关键因素，建立起各种死亡因素与种群数量变动之间相互关系的数学模式，以便更好地了解种群和预测种群的动态。特定年龄生命表中通常包括如下几项： x为取样年龄间隔或年龄级（也称虫态）; lx为年龄间隔x开始时的存活数；d_x为年龄间隔x到x+1中的死亡数；d_xF为与d_x相对应的死亡原因；100 qx为死亡百分率； S_x为在年龄间隔x内的存活率。N₁、N₂分别为第一、二代起始虫数。

表 3 松干蚧第一代生命表（郑汉业等）

虫 态	开始 存活数	死亡原因	死亡数	存活率	死亡率
x	lx	dxF	dx	Sx	100qx
卵(N1)	142.10 139.68 107.98	不孵化 花蝽捕食 卵囊随风离去	2.42 31.70 43.98	0.983 0.774 0.593	1.7 22.6 40.7
若 虫 （隐蔽期）	64 00 44.30 8.10	花蝽捕食 树木抗性和高温 大赤螨捕食	19.70 36.20 2.50	0.692 0.183 0.691	30.8 81.7 30.9
若 虫 （显露期）	5.60 4.50	树木抗性 无敌捕食	1.10 1.60	0.804 0.645	19.6 35.5
成 虫	2.90 1.79 0.45 0.20	蜘蛛、蚂蚁捕食 雄成虫离去 花蝽、大赤螨捕食 病死和其他	1.11 1.34 0.25 0.10	0.618 0.252 0.456 0.500	38.2 74.8 55.5 50.0
卵(N2)	20.26

表中数据表明：种群增长指数 I=N₂/N₁＝0.143，即第二代种群数量下降。表中年龄级x ，不是按等长的时间划分，而是按昆虫生活史的各阶段划分。dxF一栏尽可能记载各种引起死亡的因素，以及这些因素引起的死亡数dx，成虫期如雌雄能多次交配，则按雌雄比计算出实际雌虫数，乘以每雌实际产卵量，作为总卵量，如雌雄只能交配一次，取性比为1:1，多余雌虫应为无效（性比死亡）。生命表中记录的资料可以从卵到卵为1个世代，也可以从成虫到成虫。表中
l_x+1=l_x-d_x,100q_x＝d_x/l_x×100。特定年龄生命表的特点是对 一定数量的同龄个体群进行连续观察，跟踪其全过程，直到最后一个个体死亡为止，所以这种生命表也称为同龄个体群生命表或水平生命表。
世代平均生命表 由查巴奇(R.Chubachi)1979年提出，用于世代半重叠的昆虫种群动态的研究。在世代平均生命表中.平均世代时间为：

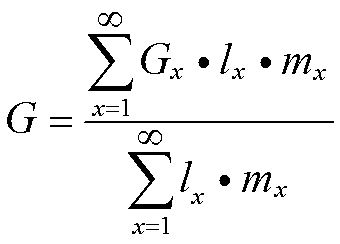
式中 G_x为卵阶段开始到第x次产卵的持续期；l_x为存活到第x次产卵的概率；m_x为在第x次产卵中每雌产下雌性卵的平均数。在平均世代时间内种群增长率为：

式中 N_t为时间t时的种群大小，N_t+G为时间t+G时的种群大小。当l_x和m_x值保持稳定时，年龄的组配也稳定。R可以近似地表示为：

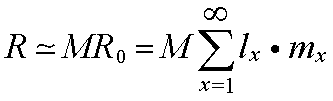
式中 Rc为净出生率。M为迁移引起种群变化率。用此方程表示种群的变化，世代愈完全重叠，方程表示愈精确，但也可用来表示世代不完全重叠的昆虫种群。当参数l_x和m_x不是常数时，R值可以用平均世代时间内所存在的全部世代的参数均值近似地给出。这些参数以均数表示，故称为世代平均生命表。

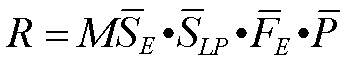
式中 S_E和S_LP分别为卵、幼虫和蛹存活率。FE为期望生育力（一个雌虫羽化后的生命期内所期望产下的总卵数）,P为雌虫的比例。世代平均生命表可写成下面的形式(表4)。

表4 世代平均生命表

x	lx	mx	lxmx
1 2 3 4	1.000l1 0.606l1 0.033l1 0.000l1	1.000m1 0.855m1 0.728m1	1.000l1m1 0.518l1m1 0.024l1m1
			Ro=1.542l1m1

世代平均生命表的参数估计与特定时间生命表相比较，受年龄分布的影响较小，因此更适合于年龄分布不稳定的种群。平均世代时间是主要的种群参数，它的估计值是在假设l_x对l₁的比值、m_x对m₁的比值在整个繁殖季节中是常数的基础上估计的。但任何一个自然种群；这两个比值多少都是变动的。只要l_xm_x曲线有一个清楚的单峰，平均世代时间的估计值误差就不会太大。
资料的获取与处理 ❶选择正确的时机对种群抽样收集数据。对世代离散的昆虫自然种群，卵、幼虫（若虫）、蛹、成虫都有明显峰期，在这些虫期的相应时间抽样，就可得到各虫态的数量资料。其前提是对该种昆虫的生物学、生活史要有详细的了解，野外调查中龄期和发育阶段的鉴别尤为重要.依据种群的空间分布型确定正确的抽样方案，并根据生命表的要求记录调查数据，然后编制成生命表。在某些季节，或昆虫种群的某一世代，自然种群密度很低，抽样调查往往收集不到生命表编制所需要的数据，在这种情况下，可采用人工补充虫源的方法，依据各虫态在田间的发育进度，移入一定数量的同龄个体，观察记录其数量变化及引起变化的因素，编制成生命表。
❷对世代不完全重叠的种群，从反复调查的数据中计算lx值。在个体数量调查中，因各种发育阶段的个体混杂存在，要从中算出达到各个发育阶段的个体数lx，可用平均龄期法或曲线下面积法。
平均龄期法 以等距离时间间隔对种群抽样，从多次调查中合计出各龄期的个体数，称为各龄的发育范围头数，乘以调查间距（天数）与平均龄期历期（天数）的比值，得出各龄历期中的个体数（设在各龄历期内死亡是等概率的）。

式中，平均龄历期为第i龄高峰与第i+1龄高峰的间距。
曲线下面积法 选择适当的时间间隔，对种群抽样，把各虫态的连续调查数分别标在方格纸上，每一小方格代表每天一个个体，连结各点绘出各虫态的个体数消长曲线，计算曲线下面积作为“发生范围头数”，除以平均龄历期，得到各龄中期的个体数。此法调查间距町以不定，但一般不宜长于各虫态的平均历期，世代必须是不连续的。

---

生命表life table

记载种群中一定数量的个体出生后随时间推移逐步死亡的表格。皮埃尔 (R.Pearl) 1921年首先用这种方法，研究了果蝇实验种群。此后，迪维 (E.S.Deevey) 1947年用生命表方法研究了某些生物的自然种群。随着统计学方法和年龄鉴定技术的进展，60年代以来，生命表应用更加广泛。通过生命表分析可了解各年龄组（或发育阶段）的存活率和死亡率，发现种群生存中的关键时期，预测平均余年。
类型 根据搜集数据的方法，可将生命表分为三种类型： ❶静态生命表。又称特定时间生命表，是在某一时刻对种群年龄组成和数量进行调查后编制的生命表。缺点是没有考虑各年龄组经历着条件各异的不同年份。
❷动态生命表。又称同一群生命表，是跟踪观察同一时期出生个体的全部生死过程而编制的生命表。缺点是在自然界长时间跟踪为数众多、同时出生的个体很困难，并且所提供的仅仅是过去一代的状况，这种生命表较少采用。
❸综合生命表。通过各种不同的方法搜集种群的年龄结构、个体死亡年龄、出生率及死亡率、雌体生育力等资料，汇总后编制的生命表。这种生命表资料来源多样、及时，为目前较多采用。每隔若干年对种群进行调查并分别编制生命表，从中寻求变化趋势，预测种群的前途可以达到相当精确的程度。
编制 在编制生命表前，首先根据不同生物的特点划分年龄或发育阶段(x)，年龄期划分越短，生命表提供的信息越详细、准确。其次是收集各年龄阶段开始时的存活数(lx)和末尾时的死亡数(dx)，其他各栏的数据根据lx(或dx)计算求出，并具有各自的含义。为表达方便，常将实际数据转化为千分数（见表）。

黑尾鹿的自然种群生命表(据Taber和Dasman,1957年的资料补充计算)^*

x	x'	lx	dx	xdx	qx	Lx	Tx	ex
0～1 1～2 2～3 3～4 4～5 5～6 6～7 7～8 8～9 9～10 10～	-100 -56 -13 31 75 118 162 206 249 293 337	1 000 474 377 240 165 145 131 117 87 52 0	526 97 137 75 20 14 14 30 35 52	263 145 343 263 90 77 91 225 298 494	526 204 363 313 121 97 107 256 402 1 000	737 426 309 203 155 138 124 102 70 26	2 290 1 553 1 127 818 615 460 422 198 96 26	2.3 3.3 3.0 3.4 3.7 3.2 2.5 1.7 1.1 0.5
			合计 1 000	合计 2 289

平均寿命=2 289/1 000=2.289年。
注： x是年龄阶段；x′是相对年龄，x′=100(x-平均年龄)/平均年龄； lx是按出生数(l₀)为1000换算的x年龄开始时的存活千分率； dx是与出生数相对的死亡千分率，dx=lx-₁-lx; qx是各年龄阶段开始时作1 000计算所得的死亡千分率，qx=1 000dx/lx; Lx是x年龄阶段的平均存活数，Lx=(lx+lx+1)/2; Tx是个体年累计，Tx=Lx+Lx+1+Lx+2+……； ex是x年龄阶段个体的平均余年估计值 （人寿保险公司利用该值计算保险费率）,_ex=Tx/lx。
存活曲线 根据生命表提供的数据，以时间（年龄或相对年龄）为横座标，各年龄组存活数lx为纵座标所作的曲线。lx用对数标尺，相对年龄x′作时间单位，则可把平均寿命相差很大的生物归纳在一个座标系中进行比较。存活曲线更直观地表达出种群各年龄组的死亡过程。根据存活曲线的形状，迪维把它划分为三种类型： ❶a型。接近平均年龄之前的幼体死亡率低，然后急剧上升，呈凸形。大型哺乳动物、猛禽及有护仔行为的某些昆虫多属此类。
❷b型。各年龄组间死亡率基本相等，呈线形。多数昆虫、某些爬行类、小型鸟兽属于此类。
❸c型。接近平均年龄之前幼体死亡率很高，其后较低呈凹形。多数鱼类属于此类。研究存活曲线的类型对分析种群动态是很有用的。在生物界，存活曲线有从c型→b型→a型的进化趋势，并有许多中间类型（见图）。

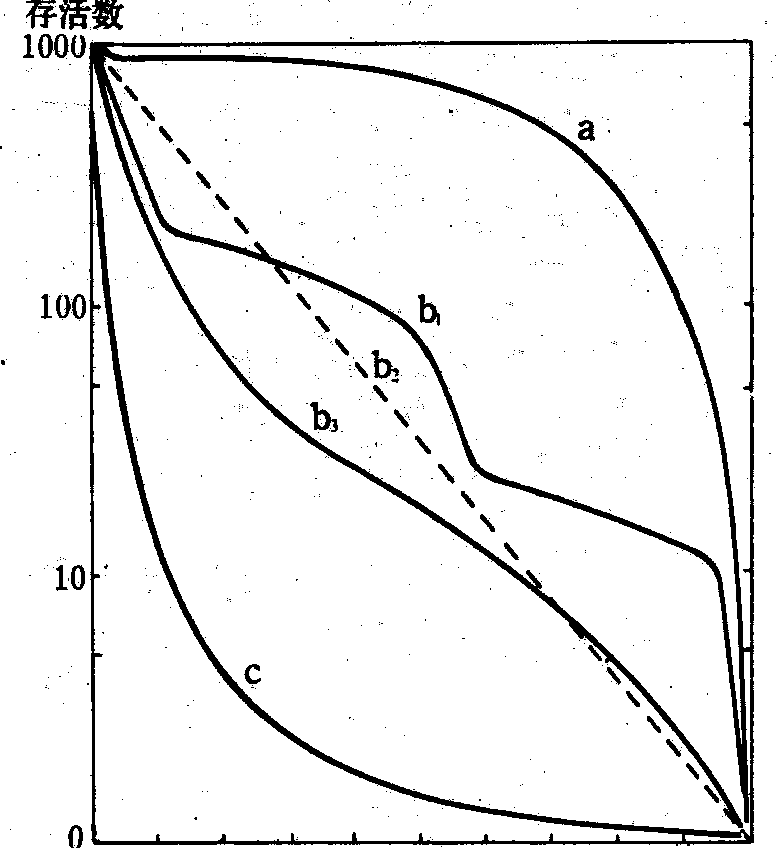
年龄—平均寿命的百分比

存活曲线的几种类型
a: 凸形存活曲线，多数在接近生命期末死亡； b1: 阶梯形，生活史中存活率变化剧烈； b₂: 理论曲线（直线）; b₃: 接近b2的S形；c: 凹形，幼体期的死亡率高

生命表life table

根据种群的年龄结构、各年龄组的存活数、死亡个体数等资料编制的研究种群生存和死亡过程的表格。通过生命表的分析可以了解各年龄组（或发育阶段）的存活率和死亡率，发现种群生存中的关键时期，预测平均还能存活的年数。生命表是反映种群数量变化的收支簿，也是研究种群数量动态的一个重要手段。

生命表

根据某种群内个体死亡和生存的数据编制的、描述种群死亡过程的图表。借以推算种群的平均寿命和种群数量的发展趋势。按收集数据的方法分静态生命表和动态生命表等。

---

生命表

见“医药卫生”中的“生命表”。

---

生命表

即“寿命表”。

生命表Life Table

亦称“死亡表”，是反映一个国家或一个区域人口生存死亡规律的调查统计表。根据一定调查时期所获得的有关国家或地区的人口普查资料（或有关部门的统计资料），经过分析整理，折算成以10万或100万同年龄人为基数的逐年生存与死亡的数字编制而成。生命表以年岁为纲，全面、完整地反映了某一国家或地区一定人群从诞生直至全部死亡的生死规律。生命表的编制为经营人寿保险业务奠定了科学的数理基础，是计算人身保险的保险费、责任准备金、退保金的主要依据。世界上第一张生命表是英国天文学家哈雷于1693年编制而成的。20世纪90年代中国人民保险（集团）公司组织专家，成功地编制出《中国人寿保险业经验生命表》，并于1997年4月1日起正式运用于人寿保险业务的经营核算中。

生命表

反映某一批人从出生到随着年龄增长而陆续死亡的整个生命过程的统计表。又称死亡表或寿命表。生命表的基本内容如下：

年龄x	死亡 概率 nqx	尚存 人数 lx	死亡 人数 ndx	生存 人年 数nlx	x岁以上生 存人年总 数Tx	平均预期 再生存年 数e
0 1 2 · · · 99 100 · · ·

表中，年龄(x)指某一确切年龄或某一年龄组，死亡概率(nqx)指活到确切年龄x岁的一批人在满x+n岁之前可能死亡的比率。尚存人数(1x)指同期出生的一批人活x岁的人数，死亡人数(ndx)指活到x岁的人当中在今后n年内死亡数。生存人年数(nlx)指某一确切年龄x岁与另一确切年龄x+n岁之间一共生存过的人年数。在一岁一组的生命表中，某一岁的生存人数也就是在这一岁中平均生存人数。某确切年龄x岁以上生存人年总数(Tx) 即从x岁开始的各年龄组生存人年数的累计。平均预期再生存年数(e)为活到X岁的1x人今后平均每人预期尚可活的年数。因而各栏数据除死亡概率要根据当时某人群的死亡率水平计算外，其他数据等均为理论数据。生命表可以全国编，也可分地区、分城乡编。但地区范围不宜过小。由于男女死亡率有相当差异，编制时一般为男、女两部分，也可以单独编。编制生命表通常根据某一时期 （如一年或连续几年） 的分年龄死亡率，所以这样编出的生命表实际是反映某一时期的分年龄死亡水平。生命表是研究人口再生产问题的重要工具，它能预测在现有的社会经济，科学技术、环境与卫生条件下人口的平均寿命； 能为考察人口再生产状况，计算净人口再生产率和世代平均间隔年数、预测未来人口数量及构成的变动、制定长期人口规划提供科学的数据。并为规划劳动就业、社会福利、文化教育和医疗卫生事业提供人口要素的重要资料。

生命表

又称“死亡表”、“死亡率表”，根据分年龄死亡率编制，反映一批人 (通常为10,000人) 从出生后陆续死亡的全部过程的一种统计表。生命表内容有：
❶当年生存者的年龄，用符号X表示；
❷生存人数，以一定的出生数为基数，生存至X岁的人数，用符号LX表示；
❸死亡人数，X岁的人在一年内的死亡人数，用符号dX表示；
❹死亡率，X岁的人在到达X+1岁前的死亡机率，用符合qx表示；
❺生存率，X岁的人到达x+1岁时仍然生存的机率，用符合px表示；
❻生命期望值，x岁的人以后还要生存的平均年数。生命期望值也叫平均余命。零岁人的平均余命就是平均寿命，用符合ex表示。

生命表life table

亦称“死亡表”、“死亡率表”、“寿命表”。根据各年龄的死亡率编制的，反映某一数量(通常为10万或某一大数)同时出生的人所组成的群体，自出生起一直到该群体生存人数为零时止的期间，以统计数字表明其每年的生存、死亡状态的统计表。包括的内容有：
❶lx，代表生存到x周岁的人数。
❷dx，代表x周岁的人在活到x+1岁之前死亡的人数。
❸q_x，代表x周岁的人在x+1岁之前死亡的死亡率。q_x＝dx÷lx。
❹p_x，代表x周岁的人活过x+1周岁的生存率。p_x＝(lx-dx)÷lx=1-dx÷lx=1-qx。
❺e_x,x周岁的人平均尚能生存的年数，称为平均余命，亦称平均寿命，刚出生的人的平均余命即为通常意义上的人均寿命。
❻Lx,x周岁至x+1周岁之间生存的平均人数。
❼Tx,x周岁以上年龄段生存人数的总平均人数。

生命表

根据分年龄死亡率编制的，反映一批人(通常以10万人或100万人为基础)从出生后陆续死亡全部过程的统计表。由于生命表的基础是分年龄死亡率，故又称死亡率表或死亡表，亦称寿命表。生命表一般是根据某一年或几年的人口死亡率编制的，它所反映的是一段时期人口死亡水平。生命表是计算人身保险费及责任准备金的基础之一。
生命表的内容 生命表表明同时期出生的一批人陆续死亡减少的全过程，其基本内容有：
❶年龄。从出生时起到计算时止所经历的时间，通常用“X”表示。例如，X=60，代表年龄60岁。
❷死亡人数。指在同一时期内出生者在各个年龄内的死亡人数，通常用“dx”表示。例如，年龄60岁的人，在60岁一年中死亡1149人，则表示为d₆₀＝1149。死亡人数是生命表中最基本的指标之一。
❸生存人数。指在同一时期内出生者当年能够活到各个年龄的人数，通常用“Lx”表示。例如，假定10万人到60岁时还有83678人生存，则表示为L₆₀＝83678。生存人数也是生命表中最基本的指标之一。
❹死亡率。一定时期内（通常为一年）死亡人数与同期平均人数（或期中人数）之比，即同一年龄内的人在某年龄内死亡的概率。通常用“qx”的千分比表示。表明该时期人口的死亡强度。例如，年令60岁的死亡率为q ₆₀＝d60/l60×1000‰。
❺生存率。一定时期内（通常为一年）期末生存人数与期初生存人数之比，即同一年龄的人在某年龄内生存的概率。通常用“Px”的千分比表示。例如，年令60岁的生存率为P₆₀＝L⁶1/L60×1000‰。
❻平均余命。在一定的年龄别死亡率水平下，活到年龄x岁后平均还能继续生存的年数。简称平均余命，亦称平均预期寿命或生命希望值。通常用“ex”表示。例如，60岁的人平均还能活18.03岁，则表示为e₆₀＝18.03。除以上所说之外，有的生命表还有：生命表人口数、生命表人口累积数、死亡力等内容。
人身保险对生命表的选择 决定人身保险费率的因素是利率、生命表和保险公司的营业费用。其中很重要的因素，是生命表中的死亡率与生存率。因为保险费是危险的代价，在死亡保险里，保险费计算主要建立在预定死亡率基础上。预定死亡率愈高，危险及其代价就愈大，故保险费愈高；反之，预定死亡率愈低，则危险及其代价就愈小，其保险费愈低。死亡保险的保险费高低，与生命表中死亡率的高低成正比例关系。生存保险的保险费与生命表中的生存率成正比，与死亡率成反比。
在人身保险业务上，不仅保险费的计算需要生命表，在责任准备金计算、业务报表分析、人身保险盈亏分析上同样需要利用生命表。没有人类对人口死亡率的探讨，没有生命表就没有科学的人身保险事业。
生命表的种类 依编制生命表的对象分类，有国民生命表（由政府有关部门或科学工作者根据全国家或某一地区的人口调查统计资料编制而成）、经验生命表（根据一家或数家人寿保险公司在历年业务中所积累起来的关于被保险人死亡统计资料编制而成）和模型生命表（根据许多国家不同的实际死亡率水平编制的一套具有代表性的生命表）。依编制生命表的方法分类，有完全生命表（根据人口死亡资料依照每个年龄为一组编制）、简略生命表(按5岁或10岁为一年龄组直接根据各年龄组死亡率编制)和选择生命表(同时考虑被保险人的年龄与保险年数两种因素，由几个生命表经过选择编制而成)、终极生命表（按选择期终止时的死亡率编制）和综合生命表（仅按被保险人的年龄编制）。依编制生命表对象的性别分类，有不分男女性别的混合生命表、男性或女性生命表。
保险公司在进行人身保险业务时，为了获得稳定的经营，往往根据经营不同的保险险种得到的死亡率，编制出不同类别的生命表。如承保年金保险所用的团体年金生命表、个人年金生命表，还有承保一般人寿保险业务所用的普通寿险生命表等等。

生命表

亦称“死亡表”。人口生存或死亡规律的调查统计表。它反映同一年龄的一群人每年生存或死亡的概率。通常以某一时期现时人口的分年龄死亡率为基础进行编制。生命表的编制方法，是假定同龄一批人，按照某一人群现时的分年龄死亡率而测定的死亡概率，先后陆续死去，直到全部死亡。表明这一过程的生命表的基本内容和表式如下：

生命表

编制生命表的步骤和方法是： (1) 根据某一年 （或几年） 分年龄、性别的人口数和死亡数资料，计算分年龄死亡率，并据以计算死亡概率填入第 (1) 栏。(2) 将假定同时出生的一批人 (通常定为10万) 填入零岁组第 (2) 栏，作为这一批人 （即尚存人数）的起点。(3) 以死亡概率乘以尚存人数，将所得死亡人数填入第 (3) 栏。(4) 用某年龄组尚存人数(Ix) 减死亡人数 (dx)，得到比该年龄大一岁的尚存人数 (Ix+1)，填入下一岁的第 (2) 栏。(5) 以某年龄组尚存人数 (I_x) 与比该年龄组大一岁的尚存人数(Ix+1) 相加除以2，求得该年龄组平均尚存人数(Lx=1/2 (Ix+Ix+1)，填入第 (4) 栏。零岁组内死亡人数不是呈均匀分布，差异较大，其平均尚存人数一般按L0=1/3I0+2/3I1计算。(6) 未来生存人年数累计 (T_x) 为某年龄组和该年龄组以上各年龄组平均生存人年数的累计数。如 Ta5=L95+L96+L97+L98+L99+L100。(7) 以某年龄组未来生存人年数累计除以该年龄组尚存人数，便得到该年龄组平均预期寿命： Tx/Ix=ex。在编制全国 (或省、市、城、乡等) 生命表时，由于不同性别的分年龄死亡率有在差异，一般都包括男子、女子和男女合在一起的三种类别的生命表。世界上最早的一张生命表，是英国天文学家哈雷 (Edmund Halley,1656—1742) 于1693年制成的。目前在保险经营中广泛使用的，是1958年美国根据15家规模较大的人寿保险公司在1950—1954年签发的标准普遍寿险保单，经过统计，分析、整理而编制成的经验死亡表，简称C.S.O.生命表。

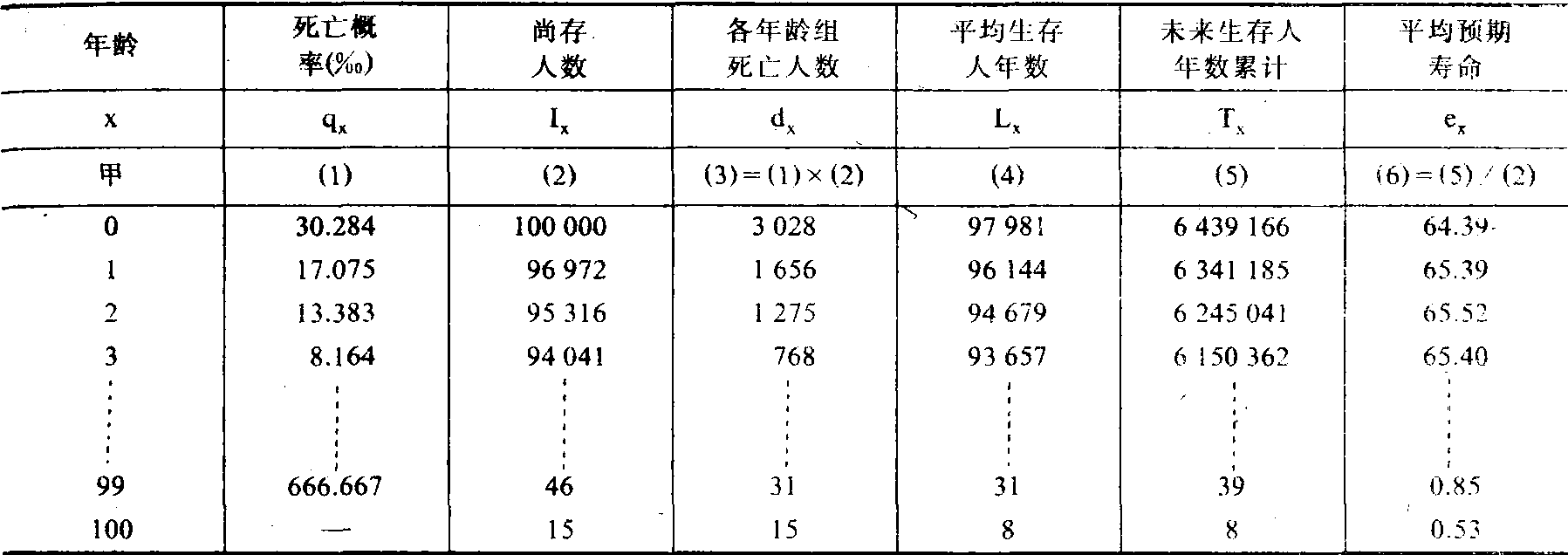
生命表

life table

---

生命表

life table