生产函数

生产函数指厂商在一定时期内所使用的各种投入的数量与它所能生产的最大产量之间的一种依存关系。用公式表示即是：

Q=f(L、K、N、E)

式中Q表示产量，L表示劳动，K表示资本，N表示土地，E表示企业家才能，f表示一种函数关系。此公式的含义是，在一定期间内，在生产技术基本不变的条件下，产量是劳动、资本、土地和企业家才能这四种生产要素不同组合的函数。
生产每一单位产量所需要的生产要素的数量，可能是固定的，也可能是可变的。根据生产要素的配合比例是否固定，生产函数可以分为两种类型，即固定比例生产函数和可变比例生产函数。在可变比例生产函数中，生产过程中的一种生产要素可以用另一种生产要素来代替。西方经济学认为，生产函数是一种技术关系，在特定的技术条件下，存在特定的生产函数，技术条件改变了，生产函数也会改变。凡技术系数为变量的生产函数，都要受边际效益递减规律的支配。即在其他生产要素的使用量不变的情况下，若某一生产要素的投入量增加，则该生产要素的边际生产力最终必然下降。据此规律，企业就必须选择合理的投入及投入区间，才能保证利润的获得。换言之，面对投入与产出之间的这种依存关系，厂商理性的决策就是确定一个他所购买的两种生产要素数量的组合，以便用最低的总成本来生产既定数量的产品，或者，使花费给定数量的总成本所生产的产品量为最大。
从另一方面来看，生产函数还表明，收益是随生产规模的变化而变化的，即产量随各种生产要素的增加而增加。在各种生产要素按固定比例增加时，如果产量也以相同的比例增加，称为规模收益不变，此时的生产函数为线性齐次函数； 如果产量增加的比例大于生产要素增加的比例，称为规模收益递增； 如果产量增加的比例小于生产要素增加的比例，称为规模收益递减。据此规律，厂商必须选择适度规模。
生产函数可以表示一个企业的技术状况，也可表示一个社会的技术状况。

生产函数Production Function

指生产诸要素在生产中的消耗量与所得到产量之间相互关系的方程式。假设运用最有效的生产方法，运用这种方程式就可以计算出生产要素各种组合所能生产的产量。它既能测出一定的生产要素的边际生产率，也能计算出既定产量的各种要素的最佳的经济组合。

生产函数Production Functions

描述产出与投入之间最佳技术关系的一种函数。它表示一组既定的投入与其所能生产的最大产量之间的关系，或者既定的产量与其所需的最小投入量之间的关系。生产一定的产出需要的投入很多，在经济分析中通常把这些投入归结为劳动、资本、土地等。在讨论中往往又把资本与土地统称为资本。因此，在经济分析中通常所讨论的是资本与劳动两种要素投入的情况。如果用多种投入生产一种产品，那么生产函数可以表示为：

Y=F (x,t)

其中，Y表示产出量，x_I(I=1,2，…，n) 表示几种投入物的数量，用投入向量X表示X=(X₁,X₂，…，X_n),t为技术水平指数。以上是生产函数的最简单而又最一般的表达形式，每一种具体的生产函数都由其具体假定而呈不同的特征。可以用从多方面来刻画生产函数的特征，例如齐次性、替代性、技术变化的特征等。如果对生产函数施加一些限制条件，则可以由生产函数推导出价格函数、成本函数，进而推导出投入函数、要素需求函数与产出供给函数，而且价格函数与生产函数具有对偶的特征，成本函数也与生产函数具有对偶的特征。

生产函数

表明在既定的技术水平下，生产要素投入量的组合与产品的最大产量之间技术关系的函数。它既可以用于描述某个企业或行业的生产特征，也可以作为总生产函数应用于整个经济。在新古典经济学的生产分析中，通常把企业视为将投入组合转化为产出的“黑匣子”，生产函数就是对企业的这种功能的量化描述。生产函数所表明的是一种技术关系。在任何技术条件下，都存在一个与之对应的生产函数。为研究方便，通常假设生产函数满足如下假定：(1) 单值连续函数，具有连续的一阶和二阶偏导数；(2) 严格凹函数或严格拟凹函数；(3) 递增的函数。在经济分析中，一般把生产函数视为劳动(L)和资本(K)的函数。最常用的生产函数是科布-道格拉斯生产函数，公式为：Q=AL^αK^β其中A是参数，L和K分别是劳动和资本的投入量，α和β的取值均大于0小于1,Q表示产量。生产函数通常可分为短期生产函数和长期生产函数。对于短期生产函数来说，至少有一种生产要素的投入量是固定不变的，产量的变化完全取决于可变要素的投入水平(通常把资本视为短期固定的生产要素，把劳动视为可变的生产要素)；对于长期生产函数来说，所有的生产要素都是可变的。

生产函数

现代资产阶级经济学中的一个基本概念。表示一定量的劳动、资本、土地等生产要素的各种不同组合同它所能生产的最大可能的产量之间的函数关系。生产函数可用来表示某一生产单位的生产技术状况，也可用来表示一个社会的生产技术状况。如果生产某一单位产品所需的各种生产要素数量是固定不变的，一般称为固定技术系数的生产函数。如果生产某一单位产品所需的各种生产要素数量是可以改变的，一般称为技术系数为变量的生产函数。后一种情况的生产函数，要受收益递减规律的制约。当生产要素的投入量按某一组合比例增加会使产量的增加大于生产要素的增加，收益会随生产规模的扩大而递增。反之，则递减。生产函数描述了物质财富生产过程中各生产要素的配合比例同产量之间的数量关系和生产要素之间的替代关系。但资产阶级经济学在运用它分析现实经济运动时，却抽掉了经济运动赖以运行的生产关系，因而不能科学揭示资本主义经济运动的实质。

生产函数Production Function

土地、劳动力、材料及设备等各种因素在生产不同数量产品中的不同组合标准。表示一定数量的各种生产投入因素所可能提供的最高产量。每一组生产函数一般表现一种技术水平，在技术水平提高后，生产函数就会改变。某一生产要素所需要的数量在生产每一单产量中有两种可能，即固定的或变动的。在变动的情况下，如果某一要素的使用率增加，那么这个要素的边际生率最后必然要下降。生产函数随生产规模的变化而使收益有所变化。如每一生产要素的投入按某种比例增加数量，就会使产量也按同一比例增加，收益也将按相同比例增加；如果全部生产要素按相同比例增加，那么产量将按大于这一比例增加，收益也将递增。相反，当产量的增加小于投入量增加的比例时，收益也会随之递减。

生产函数Production Function

要素投入量和成品产出量之间的函数关系。用以表示一定数量的各种投入物所能生产的最大可能的产量。一般可表示为：Q=f(K,L，…)。式中，Q为成品产出量，K为资本，L为劳动。它反映的是生产技术状况，即投入和产出的实物量的对比关系，而不是价值（价格）之间的对比关系。

生产函数Production Function

一种商品的产出与为生产这种商品所需要的投入（生产要素）之间的关系。它说明投入生产中的各种生产要素的任何一种组合，最多能够生产多少产出。这里要求产出最多，是指生产中不采用无效率的技术。生产函数可以用数学符号表示为：
Q=f (L,K,t，等)
式中： Q表示产出； L表示劳动投入量； K表示资本投入量； t表示 “技术进步”； “等” 表示与产出可能有关系的其他投入。虽然生产函数典型地应用在厂商理论中，但也可以说一个国家的产出依赖于用于生产此产出的各种资源，这种生产函数称为总量生产函数，其数学表达式与上面相同，除了Q代表国民 （或国内） 生产总值外，K、L等代表该国的全部资本存量和所有劳动力等资源。总量生产函数是否有意义，取决于人们对被计量的资本存量所持看法是否有实际意义。生产函数可取多种特定的代数形式。常用的生产函数有以下几种：
(1) 投入产出生产函数。这种生产函数假定产出与各种投入之间以固定的系数相联系，各种投入之间没有替代性。其函数形式为：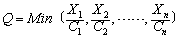

式中： Q表示产出；X₁，…X_n表示各种投入量；C₁，…C_n表示单位产出所需的各种投入的固定数量。
(2)科布一道格拉斯生产函数。这种函数形式为：
Q=AL^αK^β
式中： Q表示产出； L表示劳动投入； K表示资本投入； A为效率参数，即投入一单位劳动和一单位资本时的产出，它的数值大小受产出及投入的计量单位的影响； α为产出对劳动的弹性参数，即α=∂Q/∂K·L/Q;β为产出对资本的弹性参数，即β=∂Q/∂K·K/Q。
(3) 不变替代弹性 (CES) 生产函数。这种函数形式为：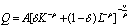

式中： Q表示产出，K表示资本投入； L表示劳动投入； A是效率参数； δ是分布参数，v是规模报酬参数；ρ是与要素替代弹性有关的参数。
生产函数的特性主要用以下概念来描述：
(1) 规模报酬。指当所有生产要素投入量都按同一比例变动时，产出量是否也按同一比例变动的问题。当所有生产要素投入量都变为原来的λ (>1) 倍时，如果产出量也变为原来的λ倍，则称为规模报酬不变； 如果产出量大于原来的λ倍，则称为规模报酬递增； 如果产出量不到原来产出量的λ倍，则称为规模报酬递减。规模报酬递减与某些投入的限制有关，特别是与自然条件的限制有关。规模报酬递增与 “不可分割性” 有关。所谓不可分割性，是指有些工艺不能低于一定投入水平之下操作。当要求较大规模投入的工艺具有较高效率、生产规模扩大到采用这种工艺时，就会发生规模报酬递增现象。规模报酬不变是最普遍的情况。
(2) 边际生产力。指在其他投入要素不变的条件下，某一要素增加一单位带来的产出增加量，即生产函数对某一投入要素的偏导数。就生产函数Q=f (L,K) 来说，劳动的边际生产力是∂Q/∂L, 资本的边际生产力是∂Q/∂K。边际生产力通常为正，即：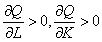

边际生产力通常随投入量的不断增加而递减。或者说，在其他投入要素不变的条件下，连续增加某一种生产要素的投入量，所带来的产出增量会越来越少，即生产函数对某一生产要素的二阶偏导数小于0: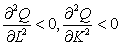

这一规律称为边际生产力递减规律或报酬递减律。它与规模报酬递减含义不同，但又有一定的关系。可以证明，当生产函数具有规模报酬不变或递减性质量，边际生产力必然递减。
(3) 生产要素之间的替代率与替代弹性。生产一定数量的某种产品，可以使用不同的资本一劳动组合来实现，也就是说，生产要素之间具有替代性。劳动对资本的边际技术替代率表示在产出量不变的条件下，增加一单位劳动可减少多少单位资本，其数值等于劳动的边际生产力对资本的边际生产力之比，用数学符号表示公式为：

替代弹性是从相对量上说明生产要素的边际技术替代率与生产要素投入比率之间关系的指标。劳动对资本的替代弹性定义为： 劳动对资本的边际技术替代率变动1%，会使资本/劳动比率变动百分之几。用公式表示为：

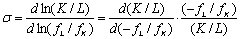
替代弹性值介于0与8之间。在市场经济中，生产要素之间的替代由要素价格的变动所引起。当工资率相对于利息率下降时，生产中增加劳动使用量，减少资本使用量就较为有利。

生产函数production function

关于生产过程中产出与投入之间物质技术关系的理论概括和抽象。用公式来表示，生产函数的一般形式为Q=f(L,K,t，……)，其中Q代表产出，L代表劳动，K代表资本，t为技术进步因素，……表示可能与生产过程相关的其他投入 （例如原材料）。生产函数分为不同的类型： 按照研究范围的不同，可分为描述单个厂商或行业的投入—产出关系的微观生产函数，和反映整个社会在一定历史时期的投入—产出关系的总量生产函数。例如柯布—道格拉斯生产函数，按照生产要素投入量结合方式的不同，又可分为固定配合比例的生产函数和配合比例可变的生产函数。
生产函数可以采取多种不同的代数形式，通常最典型的是齐次生产函数。如果一个生产函数的各种投入量乘以某一常数k，导致其产出按kⁿ倍增长，那么便称该函数为n次齐次生产函数。即，对于生产函数Q=f (L,K)，并且仅当 Q′= f (KL,KK)=kⁿ·f (L,K) 时，该函数为n次齐次生产函数。这里的n表示齐次的阶，如果n=1，该函数便叫作一次齐次或线性齐次生产函数。线性齐次生产函数显示了规模收益不变的特征，因而具有重要意义。线性齐次生产函数的例子有柯布—道格拉斯生产函数和不变替代弹性的生产函数。如果n大于1，该函数显示规模收益递增的特性。如果n小于1，则该函数显示规模收益递减的特性。

生产函数production function

生产函数是生产过程中存在于投入与产出之间的关系在技术上的说明，它用一个方程、表或图示出一个企业在每个时期用一组投入要素所能生产的商品的最大产量。投入与产出皆以实物单位计量，而不是以货币单位计量；假定技术在分析期间保持不变。它是技术关系而不是经济关系。
生产函数的一般形式是：

Q=f(x₁,x₂……x_n)

式中x₁,x₂……代表各种投入要素的数量，Q表示要素投入后能产出的最大产量，它随各种要素的变化而变化。通常，简化为两种投入要素的情况，Q=f(x,y)或Q=f(K,L),(K为资本，L为劳力)。最常用的生产函数是科布·道格拉斯(Cobb-Douglas)函数，它由道格拉斯与科布两人于1928年最早提出，其公式为：

Q=AK^aL^b

式中a与b分别为资本与劳力的产出弹性。

生产函数

表示各种必要的生产要素投入量的某种组合同它所能生产出来的最大产量之间依存关系的数学方程式或方程组。生产函数都以一个已知的技术水平为假定前提，一旦技术水平发生变化，生产函数也随之发生变化。设Q代表某种产品的产量，a、b、c……n代表各种生产要素的投入量，则生产函数的一般表达式是： Q=f (a、b、c……n)。该式表示在既定技术水平条件下，在某一时间内为生产出Q数量的某种产品，取决于所用的a、b、c……n等生产要素的投入量。西方经济学家一般把生产要素概括为劳动 (L)、资本 (C)、自然资源 (N) 和企业家才能 (E) 四种，因此生产函数一般写为： Q=f(L、C、N、E)。由于N和E的作用难以计量，所以常见的生产函数是： Q=f (L、C)。为生产出Q所需要的各种生产要素的配合比例称为技术系数。如果这种配合比例是不能变动的，则称为固定技术系数，这时生产要素之间不能替代； 反之，如果所需要的各种生产要素的配合比例是可变的，则称为可变技术系数，在这种情况下生产要素之间可以相互替代，即多用某种生产要素就可以少用另一种生产要素。技术系数可以变动的生产函数具有如下的特点： 如果让某一种生产要素固定不变，则增加使用另一种生产要素所增加的收益即生产要素的边际物质生产率迟早将会出现递减的现象。当所有生产要素同时增减亦即整个生产规模变动时，生产函数可以有三种不同类型：如果不改变技术系数扩大生产规模后，收益增加的幅度大于规模扩大的幅度，这种情形属于规模收益递增； 反之，如果收益增加的幅度小于规模扩大的幅度则属于规模收益递减； 第三种情况是规模收益不变，即规模增加的幅度与收益增加的幅度相等。下式是一个具体的生产函数实例：Q=KL^αC^1-α(K是正常数，α是小于1的正数)。该式表明在总产量中，工资的相对份额是α，资本收益的相对份额是1-α。这就是著名的柯布—道格拉斯生产函数。