球调和函数
球调和函数
球调和函数或称空间几次球调和函数是满足拉普拉斯方程: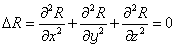
的n次齐次函数Rn(x,y,z),这里n是任何数,(x3+y2+z2)-(n+1)/2是一n-1次球调和函数。对任何维数的空间,都有类似的定义。在球坐标r, θ,φ下,Rn(x,y,z)=rnSn (θ,φ)是一个n次球面调和函数,其中Sn是cosθ,sinθ,cosφ, sinφ的多项式。共有2n+1个线性无关的n次球面调和函数,任何几次球面调和函数都是它们的线性组合。球调和函数在物理学中较多地出现。它们不仅与球坐标的拉普拉斯方程相关联而出现,而且也与球体坐标r的相应方程(球体调和函数)以及共焦点坐标F的相应方程(椭球面调和函数)相关联而出现。在几何学中,球面调和函数用于曲面论中,在数学物理学中,球面调和函数出现在引力理论、电磁理论、流体力学以及其它领域中。
☚ 约翰·冯·诺伊曼 高斯 ☛
- 黄日葵是什么意思
- 黄日通是什么意思
- 黄旦是什么意思
- 黄旭是什么意思
- 黄旭是什么意思
- 黄旭初是什么意思
- 黄旭初是什么意思
- 黄旭昌是什么意思
- 黄昆是什么意思
- 黄昆是什么意思
- 黄昆是什么意思
- 黄昆是什么意思
- 黄昆是什么意思
- 黄昆是什么意思
- 黄昆是什么意思
- 黄昆辉是什么意思
- 黄昉日是什么意思
- 黄昌是什么意思
- 黄昌孝是什么意思
- 黄昌明是什么意思
- 黄昌明是什么意思
- 黄昌有是什么意思
- 黄昌棠是什么意思
- 黄昌榖是什么意思
- 黄昌澍是什么意思
- 黄昌炜是什么意思
- 黄昌炜是什么意思
- 黄昌焕是什么意思
- 黄昌猷是什么意思
- 黄昌蓬是什么意思
- 黄昌谷是什么意思
- 黄昌贤是什么意思
- 黄昌贤是什么意思
- 黄明是什么意思
- 黄明是什么意思
- 黄明是什么意思
- 黄明亮是什么意思
- 黄明亮是什么意思
- 黄明俊是什么意思
- 黄明华是什么意思
- 黄明和是什么意思
- 黄明堂是什么意思
- 黄明堂是什么意思
- 黄明堂是什么意思
- 黄明堂是什么意思
- 黄明堂是什么意思
- 黄明堂是什么意思
- 黄明堂是什么意思
- 黄明堂(1866—1938)是什么意思
- 黄明安是什么意思
- 黄明度是什么意思
- 黄明德是什么意思
- 黄明德是什么意思
- 黄明志是什么意思
- 黄明振是什么意思
- 黄明智是什么意思
- 黄明朗是什么意思
- 黄明河是什么意思
- 黄明泉是什么意思
- 黄明洲是什么意思