独立性检验

关于两个对象(事件，属性或随机变量)独立的统计假设的检验，最常用的有：一、对于大样本，是皮尔逊x²检验；二、对于小样本，是基于超几何概率的直接检验，正态相关分析和等级相关分析，在一定意义下也可以处理独立性检验问题。常被应用于测验分数统计中。

独立性检验dulixing jianyan

指以列联表形式出现的两种分类准则是否独立的假设检验。若否定假设，就认为两种分类准则之间存在关联性或相依性。列联表的记数形式见表1。

表1 K×C的列联表

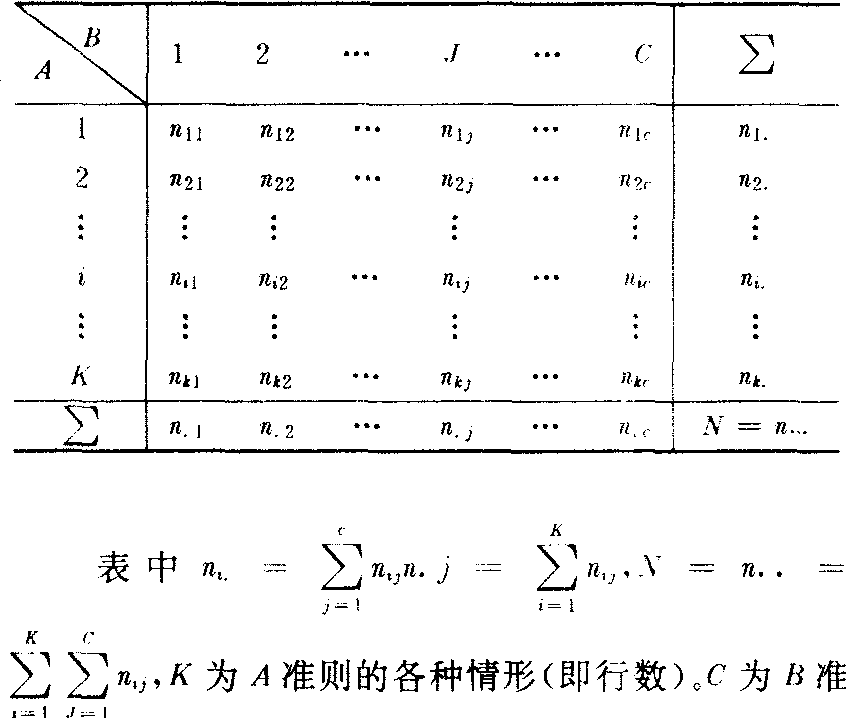
则的各种情形（即列数）。若A、B独立，则P(A_iB_j)=P(A_i)P(B_i)，而P(A_i)=＝n_i/N、P(B_j)=＝n_.j/N；实际观测次数为n_ij,相应的理论次数fe=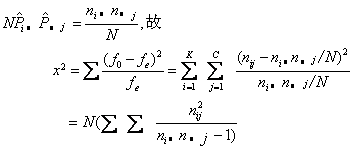
它服从于自由度为(K-1)(C-1)的X²分布。
[例] 调查家庭经济状况为上、中、下三类的高中毕业生150人，他们对于报考师范大学的态度亦有三种：愿意、不愿意、未定。其人数分布情况如下。问学生对报考师范大学的态度是否与家庭经济状况有关？

报考态度 经济状况	愿意	不愿意	未定	∑
上	18(20.9)	28(19.8)	10(15.3)	56
中	20(21.7)	18(20.5)	20(15.9)	58
下	18(13.4)	7(12.7)	11(9.8)	36
Σ	56	53	41	150

设H₀学生报考师范大学的态度与家庭经济状况独立（或无关）。若用前部分公式计X²值，则先计理论值f_e＝ni._n.j/N，并把结果写入表中括号内；若用后部分公式计（此法较为准确），则可直接代入公式：

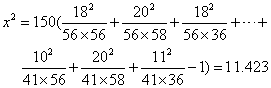
依f=(3-1)(3-1)=4及a=0.05查X²分布表得X(_4)0.052=9.49，因X²>X(4_)0.052,故拒绝H0，即学生报考师范大学的态度与家庭经济状况有关。
在表1中，当A、B均为二种可能性时，表1为2×2的列联表（见下表）。此时可用下式计X2值：

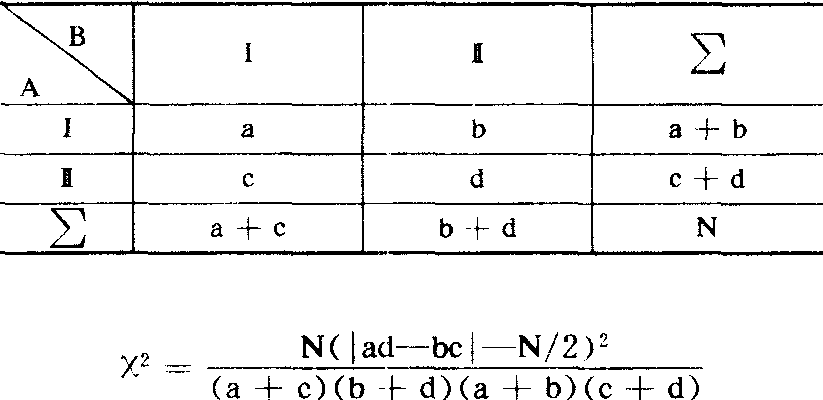
当检验结果为拒绝H⁰时，则可用下式计算这两种分类准则之间的关联程度

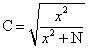
式中 X^2——所计得的值
N——总次数
C——列联系数
在上例中把X²＝11.423及N=150代入上式得：

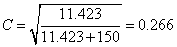
此处无需对C再作显著性检验。列联系数是两类准则关联程度的一种测度。

独立性检验test for independence

主要用于研究两个或两个以上因素多项分类之间关联性和依存性问题的假设检验方法。如人的性别和血型之间是否相关。过程是选择一组研究对象，按照不同标准对其进行分类，分析不同类别中的对象分布次数之间是否存在一定倾向或规律。常通过χ²检验进行。