物不知数Wubuzhishu

在中国四、五世纪的《孙子算经》中，有一个脍炙人口的“物不知数”问题(卷下第26题)，原题是：“今有物，不知其数。三、三数之剩二，五、五数之剩三，七、七数之剩二。问物几何。”用现代的记法，这相当于求解下面的一次同余式组 (参见 “孙子定理”):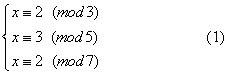
书中给出了这一问题的最小正整数解x=23, 并且给出了解法：“三、三数之剩二，置一百四十； 五、五数之剩三，置六十三； 七、七数之剩二， 置三十。并之，得二百三十三。以二百一十减之，即得。凡三、三数之剩一， 则置七十； 五、五数之剩一， 则置二十一； 七、七数之剩一， 则置十五。一百六 (注： 106) 以上， 以一百五减之，即得。”这段话的前半段给出了本题的解：
x=70×2+21×3+15×2-105×2=23后半段给出一次同余式组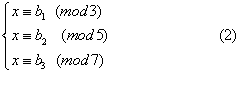
的一段解：
x≡70b₁+21b₂+15b₃ (mod3×5×7)
《孙子算经》中没有说明这一解法的原理，但是， 由于它的构造十分明显，给后人提示了线索。如果记一个整数a的整数倍为a [M], 那么， 上述解法中的关键数字70、21、15有下面的性质：

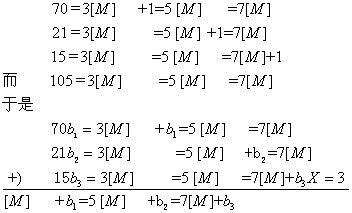
也就是说，令X=70b₁+21b₂+15b₃，那么X必然能适合同余式组(2)。选取适当的整数P，使00＝X-105P显然是(2) 的最小正整数解。这一解法的关键在于70、21、15这三个数的选取。对于更一般的一次同余式组
x≡b₁ (modm₁)
x≡b₂ (modm₂) (3)
x≡b3 (modm₃)
(其中m₁, m₂, m₃两两互素)就是要求出满足下列条件的3个数K₁,K₂, K₃:
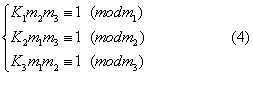
于是 (3) 的通解为
x ≡ b₁K₁m₂m₃ + b₂K₂m₁m₃ + b₃K₃m₁m₂(modm₁m₂m₃)
同余式组(2)的解法中的70、21、15相当于分别取K1=2, K2=1, K2=1。把 (3) 的解法推广到几个同余式的一般情形就是著名的 “孙子定理” （参见流条）。
现在一般认为，“物不知数”问题的实际应用背景是从汉代就已开始的推算历法中的“上元积年”，其中所用到的计算十分复杂，而“物不知数”问题仅仅是对这种算法的一种极为简略的数学概括。1247年，南宋数学家秦九韶对一次同余式组的解法进行了系统的研究与总结，不仅给出了模数m₁、_m2……m_n两两互素时解的一般形式， 对非两两互素时的情形也作了一般性的处理 (参见“孙子定理”)。
“物不知数”问题在后世引起了极大的兴趣，被收入许多数学书中， 其名称也花样繁多， 如 “鬼谷算”、“隔墙算”、“秦王暗点兵”、“韩信点兵”、“剪管术”等。人们知道对于求解 “物不知数” 问题， 关键在于求得70、21、15这三个数值， 为此还专门编制了诗歌。宋代周密 (1232—1298) 《志雅堂杂钞》卷下有 “鬼谷算”条（又称隔墙算），将其解法隐含在下面一首诗中：
三岁孩儿七十稀，五留廿二事尤奇。七度上元重相会，寒食清明便可知。
其中上元即元宵节，为正月十五， 隐15；寒食为清明前一日或二日，在冬至后105日，故寒食清明隐105。明代程大位《算法统宗》(1592)中则收入了更为直接的诗歌
三人同行七十稀，五树梅花廿一枝。七子团圆正半月，除百零五便得知。
仿照“物不知数”问题的形式，在后世数学书中出现了许多求解一次同余式组的问题，例如南宋杨辉《续古摘奇算法》(1275)中有： “七数剩一，八数剩二，九数剩三，问本总数几何。”“二数余一，五数余二，七数余三，九数余四，问原总数几何。”其解法均仿照 “物不知数”解法的构造。
晚于中国， 关于一次同余式组的问题在其他国家也曾大量出现，而且形式与“物不知数”问题十分相似。7世纪印度数学家婆罗摩笈多曾提出： “一数被6除余5，被5除余4，被4除余3，被3除余2，求此数，”约公元1000年前后， 阿拉伯学者阿尔 ·海坦 (Ibn al-Haithan)提出： “一数分别除以2, 3, 4, 5, 6，余数都是1，除以7，无余数，求这个数。”他给出的答案721并不是最小解。1202年， 意大利数学家斐波那契在《算书》中收入多个一次同余式组问题，其中有相当于下列同余式组的问题：
❶ x≡2 (mod3) ≡3 (mod5) ≡4 (mod7)

❷x≡1 (modn) n=2, 3, 4, 5, 6
≡0 (mod7)

❸ x≡1 (modn) n=2, 3, ……， 10
≡0 (mod 11)

❹x≡n (mod (n+1) n=1, 2, 3, 4, 5,
≡0 (mod7)
但均未给出一般解法。在西方，较早考虑一般解法的是德国数学家雷基奥蒙塔努斯(1436—1476)在1463年的一封信中写道： “一数除以17, 余15; 除以13, 余11；除以10，余3。知道最小数1 103已足够，因为答数有无限多个。如果加上三因数（用乘法）计算的数，就可得到第二个、第三个解。”这类问题也常以趣味问题的形式出现，例如在16世纪的一部英国算术教科书中载有“集市问题”：“一妇女赶集，蛋筐中的蛋，两个一数多一个， 三个一数多两个， 已知蛋数不超过六十个，问筐中有多少蛋。”类似的问题也出现在法国、俄国等国家的数学教科书或趣味问题集中。而对一次同余式的一般解法，则直到19世纪初才由德国数学家高斯完成 (参见“孙子定理”)。