火柴游戏Huochai youxi

利用随处可得的火柴棍，可以摆各种图形，也可以摆算式、做其他智力游戏。
例1:下图是用火柴摆出的一只蝙蝠图形，试移动其中3根火柴使蝙蝠头朝下。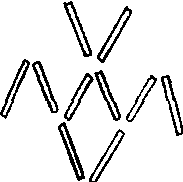
例2: 用6根火柴摆出4个边长为一根火柴长度的相同的等边三角形。
例3: 下图表示一个算式22+11=1，试移动其中一根火柴，使之变为等式。
例4: 一堆火柴共20根，二人轮流拿取， 每次限取1—2根，不准多取，也不准不取，规定取到最后一根者为胜，问先取者用什么方法取胜？又若规定取到最后一根者为负， 先取者又当如何取胜？
例5:有3堆火柴，数目依次是3根、5根、7根， 甲乙二人轮流拿取，规则是：每次限从一堆中取，不准不拿，取到最后一根者为胜，问先取者怎样取胜？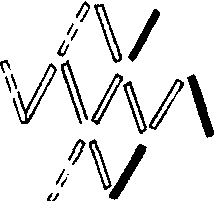
答案：1.把三根黑色火柴棍移到虚线所示位置即可。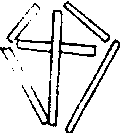
2 摆一个三角形要用三根火柴，四个三角形分开摆要用12根火柴，而现在总共只有6根火柴， 因此要有6根火柴作为两个三角形的公共边， 这在平面上无法实现， 空间中的摆放方法如图。
3.只需把算式中‘+’号的一竖移到右边即可 （如图）。
4. 按取到最后一根者为胜的规则，若剩下的火柴数被3整除， 则后取者有必胜策略， 因此先取的一方(开始时有20根火柴)第一次取2根，剩18根，此后每次取时， 注意保持剩下的火柴数目能被3整除。
按取到最后一根者为负的规则， 若乘下的火柴数被3除余1, 则后取的一方有必胜策略，在有20根火柴的情况下， 先取的一方第一次应该拿一根。
更一般的情形：有m根火柴，二人轮流拿取， 每次限取1至k根，取到最后一根者为胜，则当k+1整除m时， 后取一方有必胜策略。
5. 先来看较为简单的情形
❶若只剩2堆火柴，数目相同，那么后取者有必胜策略，办法是对方取多少，则我在另一堆中也取多少，保持两堆的数目相同。

❷两堆火柴不一样多，或者三堆火柴有两堆一样多，那么先取一方均可获胜，因为可以简单地转化到1°的格局。

❸3堆火柴依次有1、2、3根的情形，后取者可以取胜， 因为先取者不论怎样取均转变到2°的格局。这样，对于1、3、4的格局，先取方可以取胜(从有4根的一堆中取2根， 转变到1、2、3格局)。

❹三堆火柴为1, 2+2k, 3+2k的格局后取方可以取胜，这一点可以用递归的方法证明。那么，三堆火柴为1, 2k, 2k+m (k≥1, m>1)的格局，先取方可以取胜。而1, 2k+1, 2k+m (k>0, m≥1)的格局，先取方亦可取胜。
由此，可知，对于3、5、7的格局，先取一方只能在某一堆中取一根，注意到2、4、6的格局为后取方能胜。故在3、5、7时， 任取一根可保证取胜。
这种游戏有相当悠久的历史，在中国叫做抓三堆，在西方被称为Nim, 它与组合数字中的许多问题有奥妙的联系。