消毒动力学

消毒动力学主要研究消毒处理中微生物死亡的速率及有关因素对其影响的规律。1897年，Kronig等用定量方法研究了消毒对微生物的死亡情况。1907年Madsen等与1908年Chick曾将化学杀菌实验结果用数学方程式表示微生物在消毒过程中的数量变化，并认为化学消毒类似化学单分子反应。此后，研究者不断增多，根据实验结果提出了一些数学模型，有的已在发展消毒理论和指导消毒实践上起了良好作用。
消毒可看作微生物和物理化学因子互相作用的过程。微生物的种类、数量和抵抗力，周围环境的温度、湿度、酸碱度和有机物的含量，理化作用因子的种类和强度以及处理时间、方法和对象等因素，均对消毒速率和达到灭菌所需之时间产生影响。故极难使一数学模型适合所有情况。
微生物受杀菌因子作用后，其死亡数随时间延长而按对数比例增长，故其死亡速率常用半对数活存曲线表示。当杀菌因子剂量较大时，其分子在消毒过程中减少数极其微小，故可看作仅有微生物数量在改变，类似化学反应中的单分子反应即一级反应。当杀菌因子剂量小或拮抗物质过多时，杀菌因子和活存微生物同时均随时间而明显减少，则类似化学反应中的二级反应。反应不同，活存曲线亦有所不同。常见的活存曲线有：
指数活存曲线 用活存率的对数与消毒时间作图呈一直线，属一级反应曲线。微生物于整个消毒过程中，从开始到最后，死亡速率不变，正如电离辐射的每个光子或电子（子弹）击中微生物唯一致命之处（靶子）即使微生
物致死的曲线。其方程式为：1gN_t＝1gN。-Kt(N为消毒前微生物数量： Nt为消毒至t时，微生物尚活存数量)
从上述方程式可知，1gN。为直线之截距，K值为直线之斜率，即消毒速率常数。K值越大，杀灭速度越快。K值随菌种和消毒剂的种类等因素不同而异。由此方程式尚可算出杀死90%微生物所需时间，即所谓的D值。若K值用对数表示，则D值为K值的倒数。D值越大，杀灭微生物的速度越慢。由图尚可计算灭活指数(No/Nt)。消毒时间越长，灭活指数越大； 灭活指数越大，消毒效果越好。若把化学消毒或热力消毒中杀菌因子与微生物生命攸关部位的有效接触看作子弹射中靶子，则此方程式对化学或热力消毒也同样适用。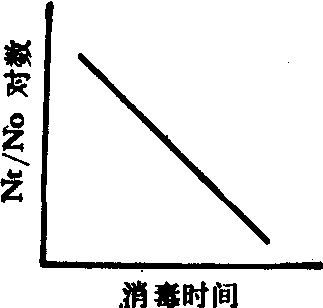

指数活存曲线

初凸型活存曲线 此类曲线表示微生物于消毒开始时死亡速率小，经一段作用时间后才呈对数死亡。Humphrey(1970) 认为其形成的原因主要是具有抗性的微生物(R)于消毒过程中先变为敏感微生物(S)然后死亡(D)。其过程图解如下：

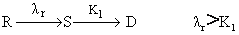
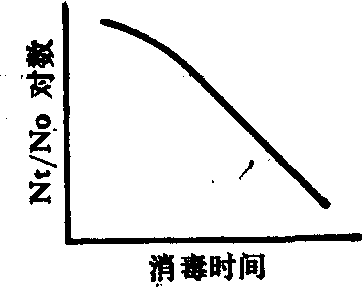
初凸型活存曲线

(λr为由抗性微生物转变为敏感微生物的速率常数；K₁为敏感微生物的死亡速率常数)
其数学方程式为：
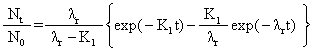
曲线初始上凸的原因尚有：
❶每个菌体上与生命攸关的部位或“靶子”不只一个，须射中多个“靶子”才死，又称多靶说；
❷被消毒的菌液中有菌块存在；
❸杀菌因子开始对微生物仅降低其新陈代谢或细胞壁的渗透性，并不立即致死；
❹微生物所受伤害，如RNA的破坏，尚可立即恢复；
❺热处理于开始时对休眠芽胞有促进发芽作用。
初凹型活存曲线 此类曲线特点为微生物在起始死亡时的速率较快，由之曲线呈一凹陷。Komenushi (1967)认为其形成的主要原因是敏感微生物和抗性微生物既可互相转变，也均可直接死亡。消毒开始时，敏感微生物形成抗性微生物的速率(λ)小，或由抗性微生物变为敏感微生物的速率(λr)较大，而后来则反之，故呈凹型。其过程图解如下：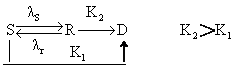

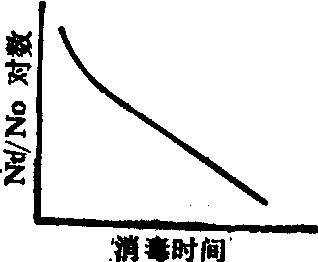
初凹型活存曲线

(K₁为敏感性微生物的死亡速率常数； K₂为抗性微生物的死亡速率常数)
其数学方程式为：
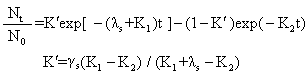
(γ为原有敏感菌菌数与原有总菌数之比值，即N/N₀)。
也有认为初凹型活存曲线的出现是因加热处理中微生物凝集成团，部分蛋白质和酶凝固的结果。
折线型活存曲线 此类曲线特点为微生物死亡的速率先后相差较大，形成一条折线。Prokop(1970) 等认为其形成的主要原因是菌群中含有两种抵抗力不同的微生物，抵抗力弱者先死，抵抗力强者后死，其过程图解如下：
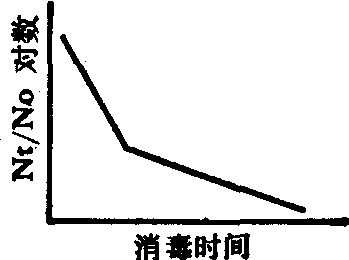
折线型活存曲线
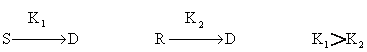
其数学方程式为：
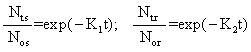
(N₀为敏感微生物原有数； Nt为敏感微生物经t时间后活存数； N₀r为抗性微生物原有数； N_tr为抗性微生物经t时间后活存数)
乙状活存曲线 此类曲线特点为微生物在起始和接近全部死亡时，其死亡速率均较小，因此形成一S状。Brannen(1968)认为其形成的原因是在消毒过程中微生物须经两步才死亡。第一步为可逆的一级反应，第二步为不可逆的一级反应。其过程图解如下：
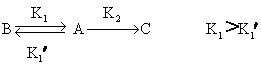
(B为原菌； A为经第一步可逆性作用之菌； C为经第二步不可逆性作用之菌； K₁、K2与K₁′为相应变化之速率常数)
其数学方程式为：
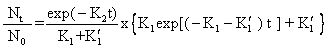
乙状活存曲线开始呈凸形，其形成的原因同初凸型曲线； 其“拖尾”现象形成的原因可能为：
❶微生物具有生理差异，例如于同一批细菌芽胞中总是约有1∶107～1∶10⁸的芽胞具有较高的抗热性；
❷消毒过程中有部分微生物适应了新环境，产生了抗性或发生了突变；
❸消毒后期于微生物周围介质中，混有细胞渗出物和死菌，对未死的微生物有保护作用；
❹微生物中有保护得更严密者；
❹消毒后期活存微生物少，活存率测定误差大。
上述为固定杀菌因子强度，变换作用时间所常见的几种活存曲线。此外，也可根据需要，固定其他因素，找出另一因素改变过程中微生物活存变化的曲线，如固定消毒时间，找出不同杀菌因子强度的活存曲线。在实际消毒工作中，可利用由曲线或方程式计算出的D值或灭活指数来预测消毒效果，设计消毒方法，控制消毒过程。如物品含菌109个，拟用D为2min的方法处理，可预计消毒10min尚有10,000个菌活存，消毒20min才达基本无菌。若电离辐射消毒中D10(见“电离辐射消毒”条)为0.3Mrad，则照射1.5Mrad尚有10,000个菌活存，照射3.0Mrad才达基本无菌。消毒后，经微生物学检查，若未达预期效果，则可说明方法或条件发生改变，如消毒时间或杀菌因子的强度不准，或温度、湿度等有较大变化。此时应找出原因，改进方法，才能保证预期消毒效果。

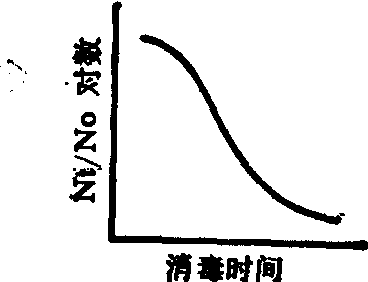
乙状活存曲线