洛必大法则
洛必大法则luobida faze
是一种利用导数求未定式极限的方法. 两个无穷小量之比和两个无穷大量之比分别称作0/0和∞/∞型的未定式,对于这两种未定式的极限求法,有如下两个洛必大法则:
法则1 (0/0型) 若函数f (x),g (x) 满足❶
❷f (z)和g (x)在x0的某个空心邻域内可导,且g′,(x)≠0,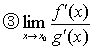 =a (或∞),则
=a (或∞),则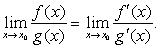
法则2 (∞/∞型) 若函数f(x),g(x)满足❶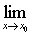
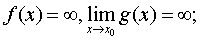
❷f (x) ,g (x)在x0的某个空心邻域内可导,且g′ (x)≠0;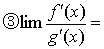 a (或∞),则
a (或∞),则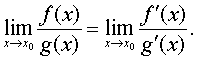
将上述法则中的x→x0换成x→x0+,x→x-,x→+∞,x→-∞时,只要对法则中的条件
❷作相应的修改,法则仍然成立.
其他未定式,如0 ·∞,∞-∞,0°,∞°,1∞,经过简单变形,都可化为∞/∞型或∞/∞型,然后再应用洛必大法则.
关于0 ·∞型未定式.若在某个过程中有f (x)→0,g (x)→∞,则作变形:
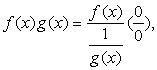
| 或 |
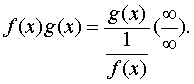
关于∞-∞型未定式.若在某个过程中有f(x)→∞,g (x)→∞,则作变形
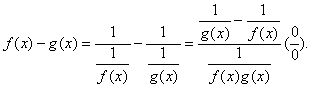
关于0°型,∞°型,1∞型未定式,可设y=f (z)g(x).于是1ny=9 (x) 1nf (x). 此时,1ny-g (x) 1 nf (x)分别为0 ·∞型,0 ·∞型,∞·0型,设在某个过程中,1ny→k,+∞或-∞. 则y→e~k ,+∞,0.
☚ 柯西中值定理 泰勒公式 ☛
- bronzino ⅱ是什么意思
- bron 布龙是什么意思
- brooch是什么意思
- brood是什么意思
- brook是什么意思
- brookeborough,basil stanlake brooke, 1st viscount是什么意思
- brooke stopford是什么意思
- brooke,rupert是什么意思
- brooke,sir james是什么意思
- brook farm是什么意思
- brookings institute是什么意思
- brooklyn是什么意思
- brooklyn 布鲁克林是什么意思
- brook peter是什么意思
- brooks,gwendolyn是什么意思
- brooks,mel是什么意思
- brooks,philips是什么意思
- brooks,van wyck是什么意思
- brook,peter是什么意思
- broom是什么意思
- broomrape是什么意思
- broomstaff是什么意思
- brop是什么意思
- brosse是什么意思
- brosser是什么意思
- brosse salomon de 布罗斯是什么意思
- brothel是什么意思
- brother是什么意思
- brotherhood是什么意思
- brotherly是什么意思
- brother’s day是什么意思
- brotulid是什么意思
- brougham是什么意思
- brough,louise是什么意思
- brouhaha是什么意思
- brouillard是什么意思
- brouwer,adriaen是什么意思
- brouwer,luitzen egbertus jan是什么意思
- brow是什么意思
- browbeat是什么意思
- browder,earl russell是什么意思
- brown是什么意思
- brown algae是什么意思
- brown bear是什么意思
- browne是什么意思
- browne,hablot knight是什么意思
- browne,robert是什么意思
- browne,sir thomas是什么意思
- brownian movement是什么意思
- browning是什么意思
- browning automatic rifle是什么意思
- browning elizabeth 布朗宁是什么意思
- browning robert 布朗宁是什么意思
- browning,elizabeth brat是什么意思
- browning,robert是什么意思
- brownist:是什么意思
- brown robert 布朗是什么意思
- brown-sequard综合征是什么意思
- brownshirts是什么意思
- brownson,orestes augustus是什么意思