正态曲线拟合

计量资料若频数分布近于正态分布，可拟合正态曲线以估计其总体分布。此法常用于重复测定误差的估计和正常值范围的估计。正态曲线拟合的方法步骤如下：
(1)计算均数X和校正标准差sc。分别按式(1)、(2)。

式中f为各组段的频数，i为组距，X₀为假定均数，x=(组中值-X₀)/i,n为样本含量，1/12为归组校正数，或称Sheppard校正数。用频数表计算标准差时，以组中值代替本组段各观察值，而组中值两侧的频数并非对称分布，而是离均数近的一侧稍多，这样算得的标准差往往略微夸大了实际的变异度。采用校正数就是为了消除此夸大的部分，使拟合的正态曲线更接近实际的频数分布。若不用频数表而直接按原观察值计算标准差，则无须校正。
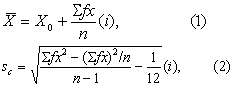
(2)计算标准正态离差u。按式(3)。

式中X为各组段上、下限。如表2资料X=14.18,sc=1.21，第一个组段的下限为10.0，因此，u=|10-14.18|/1.21=3.45，余类推，如表2第(4)栏。在X所在组段，还应写出X=X时，u=0.00。
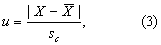
(3) 求z。由表1查出与u对应的标准正态曲线的纵坐标z，如表2第(5)栏。
(4)计算与原资料频数分布各组段上、下限相应的正态曲线之纵坐标Y。按式(4)。

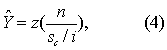
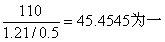式中sc/i为以组距为单位的校正标准差。如表2资料n=110,i=0.5,sc=1.21，则常数。因此，表2第(5)栏乘以45.4545即得Y，如表2第(6)栏。比如z=0.001时，Y=0.001(45.4545)=0.05；又u=0.00,z=0.399时，Y=0.399(45.4545)=18.14，即拟合的正态曲线上，X=时的纵坐标， 也就是曲线的顶点。

表1 标准正态曲线的纵坐标z

u	.00	.01	.02	.03	.04	.05	.06	.07	.08	.09
.0	.399	.399	.399	.399	.399	.398	.398	.398	.398	.397
.1 .2 .3 .4 .5	.397 .391 .381 .368 .352	.397 .390 .380 .367 .350	.396 .389 .379 .365 .348	.396 .389 .378 .364 .347	.395 .388 .377 .362 .345	.394 .387 .375 .361 .343	.394 .386 .374 .359 .341	.393 .385 .373 .357 .339	.393 .384 .371 .356 .337	.392 .383 .370 .354 .335
.6 .7 .8 .9 1.0	.333 .312 .290 .266 .242	.331 .310 .287 .264 .240	.329 .308 .285 .261 .237	.327 .306 .283 .259 .235	.325 .303 .280 .256 .232	.323 .301 .278 .254 .230	.321 .299 .276 .252 .227	.319 .297 .273 .249 .225	.317 .294 .271 .247 .223	.314 .292 .268 .244 .220
1.1 1.2 1.3 1.4 1.5	.218 .194 .171 .150 .130	.215 .192 .169 .148 .128	.213 .190 .167 .146 .126	.211 .187 .165 .144 .124	.208 .185 .163 .141 .122	.206 .183 .160 .139 .120	.204 .180 .158 .137 .118	.201 .178 .156 .135 .116	.199 .176 .154 .133 .115	.197 .174 .152 .131 .113
1.6 1.7 1.8 1.9 2.0	.111 .094 .079 .066 .054	.109 .092 .078 .064 .053	.107 .091 .076 .063 .052	.106 .089 .075 .062 .051	.104 .088 .073 .061 .050	.102 .086 .072 .060 .049	.101 .085 .071 .058 .048	.099 .083 .069 .057 .047	.097 .082 .068 .056 .046	.096 .080 067 .055 .045
2.1 2.2 2.3 2.4 2.5	.044 .035 .028 .022 .018	.043 .035 .028 .022 .017	.042 .034 .027 .021 .017	.041 .033 .026 .021 .016	.040 .032 .026 .020 .016	.040 .032 .025 .020 .015	.039 .031 .025 .019 .015	.038 .030 .024 .019 .015	.037 .030 .023 .018 .014	.036 .029 .023 .018 .014
2.6 2.7 2.8 2.9 3.0	.014 .010 .008 .006 .004	.013 .010 .008 .006 .004	.013 .010 .007 .006 .004	.013 .010 .007 .005 .004	.012 .009 .007 .005 .004	.012 .009 .007 .005 .004	.012 .009 .007 .005 .004	.011 .009 .006 .005 .004	.011 .008 .006 .005 .003	.011 .008 .006 .005 .003
3.1 3.2 3.3 3.4 3.5	.003 .002 .002 .001 .001	.003 .002 .002 .001 .001	.003 .002 .002 .001 .001	.003 .002 .002 .001 .001	.003 .002 .002 .001 .001	.003 .002 .001 .001 .001	.003 .002 .001 .001 .001	.003 .002 .001 .001 .001	.003 .002 .001 .001 .001	.002 .002 .001 .001 .001
3.6	.001	.001	.001	.001	.001	.001	.000	000	.000	.000

本表按条目“正态分布”式(4)算得。
(5)作图。 以频数表组段的上、下限X与Ŷ作图，即可绘出拟合的正态曲线（如图）。
(6)拟合优度检验。必要时可用，见条目 “频数分布的拟合优度”。
例 110名男工人的血红蛋白(g/dl)频数分布见表2第(1)、(2)栏。试拟合一正态曲线。
(1)计算与sc，按式(1)～(2)。
X₀＝14.25,i=0.5,x见表2第(3)栏，n=110,
Σfx=-15,∑fx²＝649。

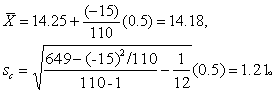
(2)求u值。见第(4)栏。
(3)求z值。按第(4)栏u由表1查得各z值，见第(5)栏。(4)求Ŷ值。按式(4):

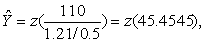
将第(5)栏各z值代入，得第(6)栏。
(5)以表2X及Ŷ作图。其中直方图是原资料的频数分布，可见拟合的正态曲线与它颇吻合。

表2 正态曲线拟合的计算

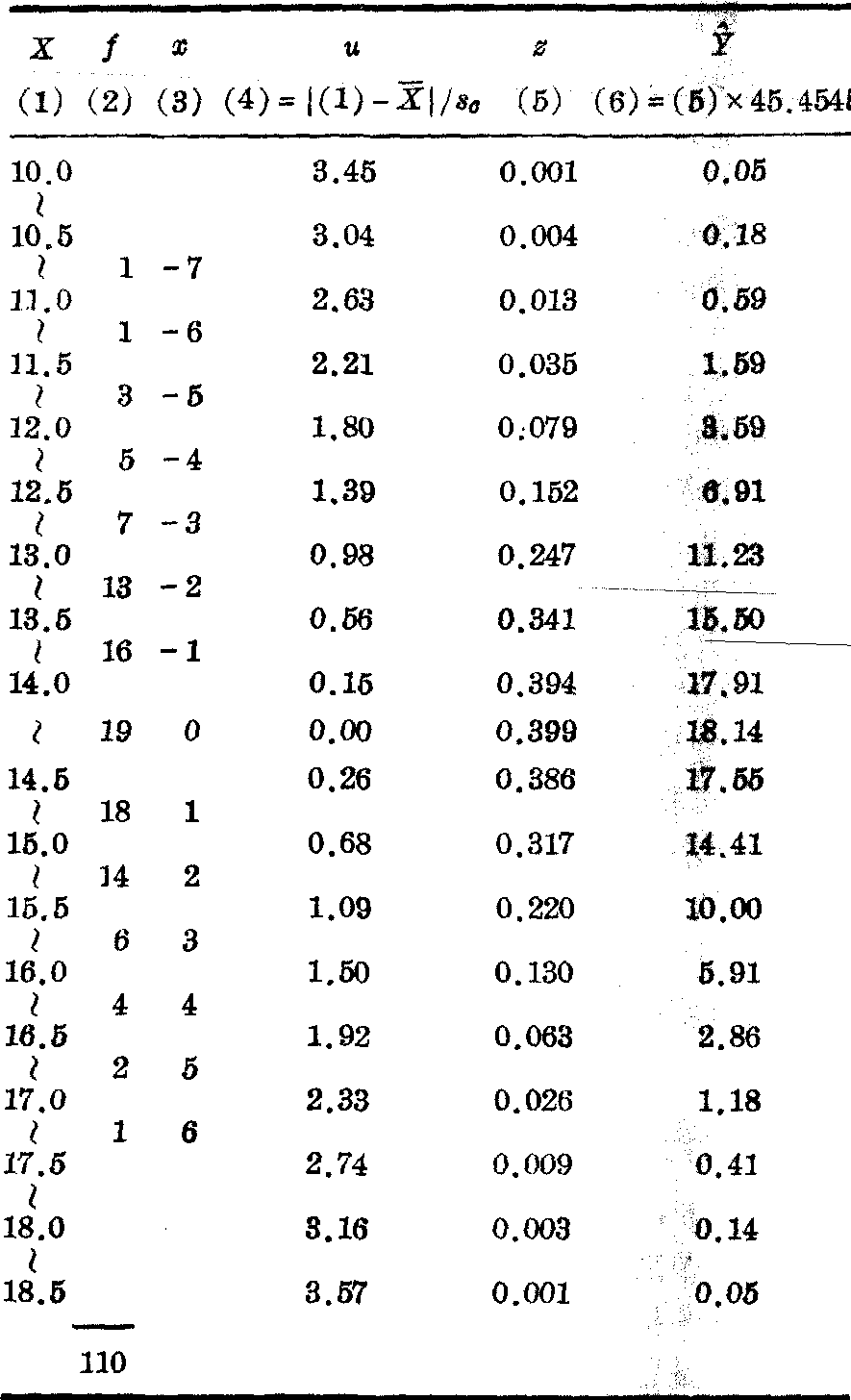
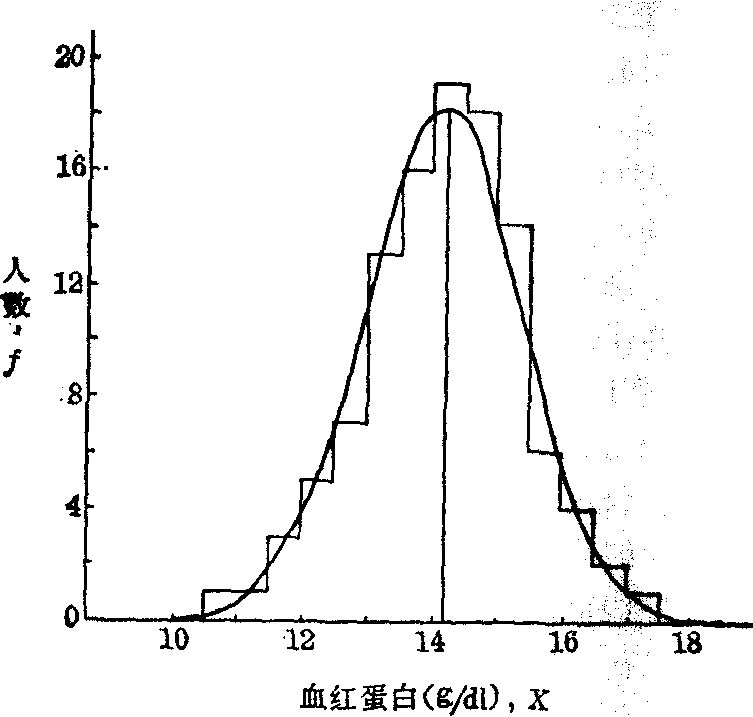
表2数据拟合正态曲线