正交试验Orthogonal Experiments

运用规格化的表格——正交表，来研究多因素试验的一种科学的方法，也称为正效试验设计。利用该方法能以较少的试验次数取得同全面试验同样的效果，且具有方法简便，便于掌握，试验效率高、效果好的优点。
正交表是具有特定性能的、规格化的工具性表格。它是正交试验中合理安排试验次数和对试验数据进行统计分析的必不可少的基本工具。正交表有三个基本概念：(1)指标，即试验指标，指正交试验中试验需要考察的效果，如产品的质量、成本、产量等；(2)因素，指对试验指标有影响的原因，这些因素中，有些可以人为地加以控制，有些则因试验条件所限而暂时未能人为控制；(3)位级，即因素的位数或水平，是指因素变化的各种状态和条件。因素在试验中所处的状态、条件的变化，可能引起指标的变化。正交表具有两个特点：(1)均衡分散性。各列中每个数字出现的次数相等，即任一因素的不同水平的试验次数相等。该特点保证了试验条件均衡地分配在配合完全的位级组合中，因而代表性强，容易出现好条件。(2)整齐可比性。任意两列对应行所组成的数字对出现的次数相等，即任意两列中全部有序数字出现相同的次数，也就是对于每列因素在各个位级上进行比较的结果之和中，其他因素在各个位级上出现的次数是相等的。这个特点保证了各个位级的效果中，最大限度地排除了其他因素的干扰，从而能最有效地进行比较并做出判断。
正交表通常以符号Ln(ba)表示。L表示正交表，a为正交表的列数，即因素数目；b为每个因素的水平数；n为正交表的行数，即试验次数。正交表有很多种类，最简单的是L4(23)，其格式如表9-4所示。常见的还有L8(27)、L18(215)、L9(34)、L27(313)、L8(41×24)、L18(61×36)等。根据每列所包含的字码种数是否相同，可以分为：(1)同位级正交表。每列包含的字码种数相同，如L4(23)。(2)混合级正交表。每列包含的字码种数不相同，如L18(61×36)等。
在进行正交试验时，首先要明确试验目的和试验要解决的问题，并根据试验目的提出衡量试验效果的定性或定量指标。在此基础上确定试验方案。包括：(1)选择因素，根据专业知识和以前的试验经验，分析影响试验效果的各个因素，找出主要的且在试验中可控的因素作为正交试验考查的因素。(2)确定位级，选择正交表。需要根据专业知识、经验、试验目的和性质确定位级（或水平），一般情况下，对于多分批的试验，可以少分级；对于少分批的试验或者重要因素，可以多分级。在分级的同时，考虑因素的个数、每批允许试验的次数、有无重点因素需详细考察等情况，选择正交表。(3)制定因素位级表。确定各个因素、位级字码、位级用量之间的对应关系。(4)安排试验计划。首先填写正交表，而后列出每个试验的具体条件，为按照试验方案中规定的条件具体操作做好准备。试验结束后，要对试验结果进行分析。利用正交试验得出的试验结果，进行多因素的优选配合，通过比较和计划，分析各个因素的不同水平对指标影响的程度，以及各个因素的重要程度等。经过反复试验，将最优的试验条件作为投产的标准工艺确定下来。

表9-4

列号 试验号	1	2	3
1 2 3 4	1 2 1 2	1 1 2 2	1 2 2 1

正交试验

正交试验是一种高效、快速的多因素试验方法。它是利用一套规格化的正交表，使每次试验的因素及水平得到合理的安排，通过试验结果的分析，获得有用的信息。医学现象一般是比较复杂的多因素问题，而各种因素本身尚有程度的差别，其间往往又存在交互作用。例如按某种指标要求摸索培养某种病毒所需的最优条件。如表1已知有四个影响因素A、B、C、D，每个因素各有二个

表1 培养某种病毒的试验因素及水平

试验因素	水	平
温度 (A) pH (B) 培养基 (C) 添加血清浓度(D)	33℃(A1) 7.0(B1) 199培养基(C1) 1%(D1)	37℃(A2) 7.4(B2) 1640培养基(C2) 2%(D2)

水平（即等级）,A₁,A₂; B₁,B₂; C₁,C₂; D₁,D₂。本试验要解决的问题是：
❶找出各因素对指标的影响，并指出哪个是主要的，哪个是次要的，哪个起独立作用，哪个起交互作用。
❷选出各因素中的一个最佳水平，组成培养某病毒的最优条件。
设计 正交试验的设计主要通过正交表。正交表是合理安排试验和数据分析的主要工具。如表2即3因素2水平8次试验的正交表。列号1、2、3可安排A、B、C三个因素，表中1、2即1水平和2水平，左列是试验号。如第1次试验A、B、C均安排1水平，第2次试验A、B为1水平，C为2水平。按此设计模型作试验。每个表的表头有一个符号，如L₄(2³)、L₉(3⁴)、L₁₂(2¹¹)、L₁₆(4⁵)等等。符号L代表正交表，L下标4、9、12、16代表试验次数，括号内的2、3、2、4代表水平数，指数位置3、411、5代表最多容许安排试验因素的个数。从表2可看到正交表有两个性质：
❶各列中不同数字出现的次数相等，如A列1与2均各出现4次；
❷任意两列同一横行的两个数字搭配均匀。如A、B两列八个横行中1、1,1、2,2、1,2、2四种对子各出现两次。以上两种性质说明正交设计充分表现了它的均衡性。

表2 L₈(2³)正交表

试验号	列 号
	1(A)	2(B)	3(C)
1 2 3 4 5 6 7 8	1 1 1 1 2 2 2 2	1 1 2 2 1 1 2 2	1 2 1 2 1 2 1 2

选用正交表的方法是：
❶根据研究目的，确定试验的因素，选出其中几种主要因素。
❷确定每个因素的水平，各因素的水平数可以相等，也可不等，主要因素的水平数可以多些，次要的可以少些。
❸根据主客观条件，决定试验次数。例如，表1是培养某病毒四因素二水平的试验。选正交表的方法是：
如只考虑A、B、C三个因素及其交互作用，可选L8(2⁷)表，表头设计如下：

列号 因素

1 A

2 B

3 A×B

4 C

5 A×C

6 B×C

7

如四个因素都要考虑，而各因素间交互作用可能不大，则使交互作用混在一起不单独提出，亦可选L8(27)表，表头设计如下：

列号	1	2	3	4	5	6	7
因素	A	B	A×B C×D	C	A×C B×D	B×C A×D	D

如四个因素都要考虑，各因素所有两两交互作用也要考虑，可选L₁₆(2¹⁵)表，表头设计如下：

列号	1	2	3	4	5	6	7
因素	A	B	A×B	C	A×C	B×C
列号 因素	8 D	9 A×D	10 B×D	11	12 C×D	13	14	15

如只考虑三个因素，不考虑交互作用，每因素的水平增到3个时，可选L₉(34)表，表头设计如下：

列 号 因 素

1 A

2 B

3 C

4

如考虑四个因素，A、B、D各取四个水平，C取二个水平，可选L₁(4³ ×2⁶)表， A、 B、 C放在前三列， D放在第4～9列中任一列，表头设计如下：

列号 因素

1 A

2 B

3 C

4

5

6 D

7

8

9

可见选用正交表时要：
❶先看水平数，如全是二水平，可选L₄(2³),L₈(²⁷),L₁₂(2¹¹),L₁₆(2¹⁵),L₃₂(²³¹) 等表；全是三水平，可选L₉(3⁴),L₁₈(3⁷),L₂₇(3¹³),L₃₆(3¹³)等表；全是四水平，可选L₁₆(4⁵),L₃₂(4³)等表； 全是五水平，可选L₂₅(5⁶)等表； 五水平以上可用正交拉丁方。水平不等时，可选L₈(4×2⁴),L₁₆(4²×2⁹),L₁₈(2×3⁷)等表。
❷根据试验要求决定试验次数。要求精确度高时，可选试验次数多的正交表； 要求精确度不高或试验条件有困难时，可选试验次数少的正交表。
❸分析的交互作用多，选列多的正交表；已知交互作用小，选列少的正交表。
❹正交表中列的占用，如果用方差分析，至少要空一列以估计误差，如用直观分析粗略估计，可不空列。
分析 正交试验的分析有直观分析与方差分析两种。1. 直观分析。将试验结果按正交表直接计算出每一因素各水平观察指标的平均值，找出各因素中最佳水平，如后例。此法可粗略地说明各因素诸水平间的差别，简单直观，但不能确切地判断各因素间的交互作用，也不能估计误差，就不能说明分析的精度。
2. 方差分析。比直观分析精确，可以补其不足。方法如下：
(1)作检验假设。有两种： 一是每一因素各水平间的比较，H₀为某因素各水平的总体均数相等； 二是分析有无交互作用，H0为两因素间无交互作用。
(2)将总变异的离均差平方和及其自由度分为各因素的各水平间、两因素的交互作用及误差等几个部分。设试验共有N个观察值X，重复试验次数为q，如表4N=40,q=5；在正交表上某因素(或交互作用、误差)各水平的重复数为r，如表3A₁重复2次，即r=2；求出各行的合计如表4“合计”栏，将与r次重复相对应的“合计”相加得K，如表5第(2)栏。则计算离均差平方和SS及自由度v的公式为：

式(3)中∑(K)2为某因素各水平K值的平方和。交互作用或误差的SS亦可仿此计算。
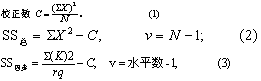
SS_误差＝SS_总减所有因素、交互作用、误差之离均差平方和，
v=总变异的v减相应各部分的自由度。
(3)分别计算各因素及交互作用的均方MS(=SS/v)，并与误差的均方相比得F值，如表6。
(4)查F界值表得P值，按所取检验水准作出推断结论。
例 在蛇毒抑瘤试验中，有三个试验因素： 蛇毒成分（峰）A、瘤株B、剂量C。A有四个水平，B、C各有两个水平：
A₁＝Ⅻ峰、A₂＝Ⅰ峰、A₃＝Ⅷ峰、A₄＝原毒，
B₁＝小白鼠肉瘤(S180)、B₂＝小白鼠艾氏腹水瘤，
C₁＝剂量0（对照）、C₂＝剂量0.075mg/kg体重。
不考虑交互作用。观察指标为瘤重(g)。试作正交试验，找出最优组合条件。
1. 设计。选用L₈(4 × 2⁴)表(表3左侧)安排试验：表3的1,

表3 L₈(4 × 2⁴)表及5鼠重复试验的合计瘤重

试验号	列 号					瘤重(g)
	1(A)	2(B)	3(C)	4	5
1 2 3 4 5 6 7 8	1 1 2 2 3 3 4 4	1 2 1 2 1 2 1 2	1 2 1 2 2 1 2 1	1 2 2 1 1 2 2 1	1 2 2 1 2 1 1 2	8.8 3.0 7.3 4.1 3.5 4.3 3.0 6.3

2,3三列分别安排A,B,C;4,5两列作为计算误差用。为减少实验误差的干扰，每次试验用5头小白鼠作重复试验。按表3，第一次试验A、B、C均安排1水平，5头小白鼠的试验结果见表4第1行； 第2次试验，A为1水平，B、C均为2水平，5头小白鼠的试验结果见表4第2行；余仿此。全部试验结果见表4 。再将表4各行 “合计”抄录于表3右侧供分析用。

表4 5次重复试验的小白鼠瘤重(g)

试验号	受试鼠号					合 计
	1	2	3	4	5
1 2 3 4 5 6 7 8	1.5 0.6 1.7 0.7 0.6 1.0 0.4 1.0	2.0 0.6 0.9 0.9 0.7 1.1 0.6 0.9	1.6 0.8 1.4 0.8 0.5 0.6 0.9 1.1	2.0 0.5 1.6 1.0 0.7 0.9 0.6 1.8	1.7 0.5 1.7 0.7 1.0 0.7 0.5 1.5	8.8 3.0 7.3 4.1 3.5 4.3 3.0 6.3
						40.3

2. 分析。
(1)直观分析。见表5，第(2)栏K为表3中每一因素各水平对应的“瘤重”相加，如表3中： A₁是安排在A列的第1、2次试验，对应的“瘤重”为8.8及3.0，相加得K=11.8; B1是安排在B列的第1、3、5、7次试验，对应的“瘤重”为8.8、7.3、3.5及3.0，相加得K =22.6；余仿此。再以每一因素各水平共用的动物数除之即得平均瘤重见表5第(4)栏。由此可直观看出，四个峰值按其抑瘤作用的效果依次为A₃(Ⅷ峰),A₄ （原毒）,A₂(Ⅰ蜂),A₁(Ⅻ蜂)；瘤株以B₂ （艾氏腹水瘤）较为敏感，剂量以C₂(0.075mg/kg体重)的抑瘤作用较好。
(2) 方差分析。
A因素四个水平间：
　H₀: μ₁＝μ₂＝μ₃＝μ₄
　H₁: μ₁、μ₂、μ₃、μ4不等或不全相等。
B因素二个水平间：
　H₀: μ₁ =μ₂
　H₁: μ₁≠μ₂;
C因素二个水平间：

表5 每一因素各水平的平均瘤重

因素及水平 (1)	总瘤重，K (2)	动物数 (3)	平均瘤重(g) (4)
A1 A2 A3 A4 B1 B2 C1 C2	11.8 11.4 7.8 9.3 22.6 17.7 26.7 13.6	10 10 10 10 20 20 20 20	1.18 1.14 0.78 0.93 1.13 0.88 1.34 0.68
41 42 51 52	22.7 17.6 20.2 20.1	20 20 20 20

H₀: μ₁＝μ₂
H₁: μ₁≠μ₂。
均取α=0.05。
由表4及表5资料，按式(1)～(3):

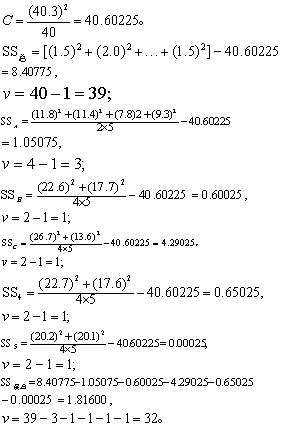
表6 方差分析

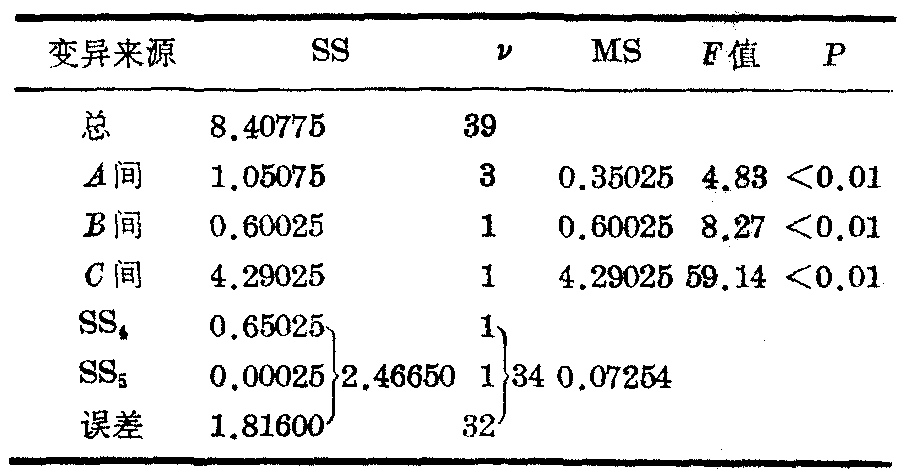
查F界值表得P值，见表6。
结论： 蛇毒组A间、瘤株B间和剂量C间，按α=0.05水准均拒绝H₀，接受H₁。表明： 蛇毒抑瘤作用以成分Ⅷ峰、瘤株艾氏腹水瘤、剂量0.075mg/kg体重的组合条件为最好。