椭圆的标准方程tuoyuan de biaozhun fangcheng

指方程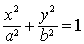(其中a>b>0).椭圆的标准方程表示焦点为F₁ (-c,0),F₂ (c,0)，满足|MF₁|+|MF₂|=2a (a>c>0)的点M(x,y)的轨迹，a,b,c的关系是b²＝a²-c²(如图1).这一标准方程的导出过程，表明“椭圆上任意一点的坐标都适合这一方程”；而“坐标适合这一方程的点必在椭圆上”.

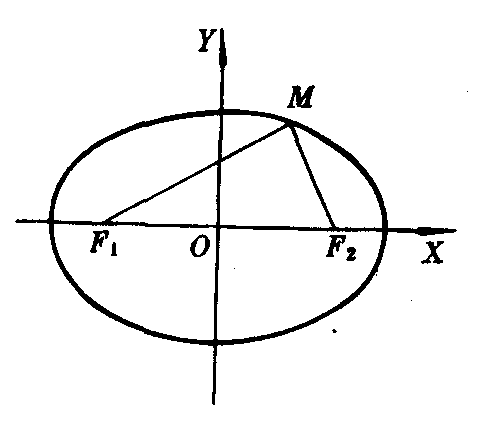
图1

图2

方程

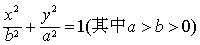
也叫做椭圆的标

准方程，表示焦点为F₁ (0,-c)和F₂(0,c)，满足|MF₁|+|MF₂|=2a(a>c>0)的点M的轨迹，a,b,c的关系是b²＝a²-c² (如图2).
椭圆的标准方程的特征是：
❶左端只含有x²项和y²项，并且系数写在分母的位置上，两项都取正号，右端只有常数1.
❷椭圆的中心在原点，焦点在坐标轴上，对称轴是两坐标轴.
中心位于(x₀,y₀)，对称轴平行于坐标轴的椭圆方

程是

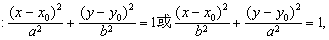
其中

a>b>0.