椭圆的性质tuoyuan de xingzhi

❶对称性 椭圆是轴对称图形，有两条互相垂直的对称轴；它也是中心对称图形，对称中心就是两对称轴的交点，叫做椭圆的中心；对称轴与椭圆的交点叫做椭圆的顶点，连结相对两顶点且过两焦点的线段叫做椭圆的长轴，连结相对两顶点且不过焦点的线段叫做椭圆的短轴.椭圆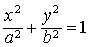的两对称轴是两坐标轴，对称中心是原点；四个顶点是A’(-a,0),A(a,0),B’(0,-b),B(0,b)，长轴A′A=2a，短轴B′B=2b(图1).椭圆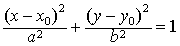的两对称轴是直线x=x₀和y=_y0，对称中心（即椭圆的中心）是(x₀,y₀)；四个顶点是A′(x₀-a,y₀),A(x₀+a,y₀),B′(x₀,y₀-b),B(x₀,y₀+b)，长轴A′A=2a，短轴B′B=2b(如图2).

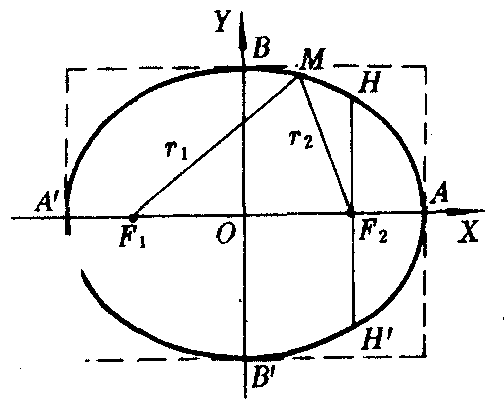
图1

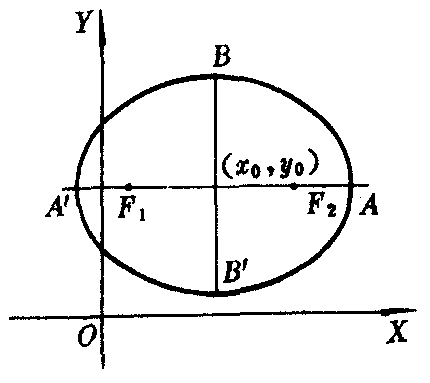
图2

❷封闭性 椭圆是封闭曲线.

椭圆

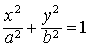位于由四条直线x=±a,y=±b围成的矩形内；椭圆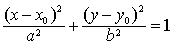位于四条直线x=x₀±a,y=y₀±b围成的矩形内.

❸形状可变性 比值e=c/a叫做椭圆的离心率.由于a>b>0，离心率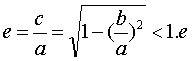接近于1,b/a越接近于0，椭圆越扁；e越接近于0,b/a越接近于1，椭圆越接近于圆.换言之，离心率e反映了椭圆的扁圆程度.比值μ=b/a也可反映椭圆的扁圆程度，叫做椭圆的压缩系数.

椭圆

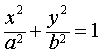
是将

圆x²+y²＝a²沿Y轴方向按压缩系数μ=b/a压缩而得的(如图3).

椭圆

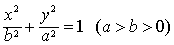
和

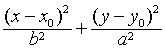＝1 (a>b>0)也有类似的性质.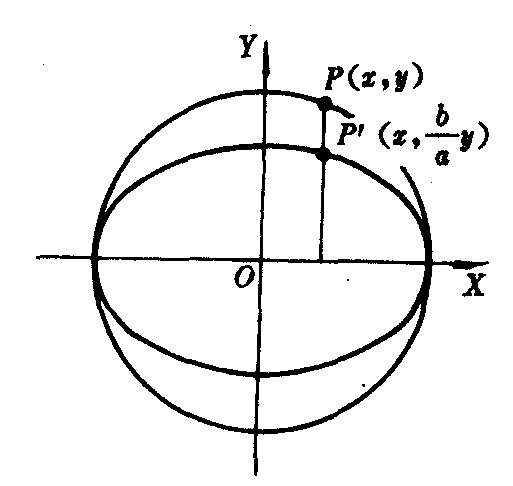

图3