最大社会福利产量Maximum Social Welfare Output

在一定偏好、技术和资源条件下使社会福利极大化的社会产量。考察一个两位消费者、两种产品、一种基本生产要素的经济。已知：
(1) 两位消费者的效用函数分别为：

U₁＝U₁(x₁₁,x₁₂,x₁⁰-x₁) (1)
U₂＝U₂(x₂₁,x₂₂,x₂⁰-x₂) (2)

式中，x_ij表示第i位消费者对j种产品的消费量，x_i⁰和x_i分别表示第i位消费者对基本要素的初始拥有量和供给量。
(2) 社会生产函数为：

F(x₁₁+x₂₁,x₁₂+x₂₂,x₁+x₂)=0 (3)

(3)社会福利函数为：

W=W(U₁,U₂) (4)

将效用函数(1)和 (2)代入 (4)，使社会福利函数从效用空间转换到商品空间，在社会生产函数(3)约束下使其极大化，即：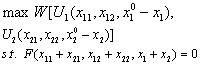

由极大化一阶条件可求出最大福利产量x₁₁^*+x₂₁^*,x₁₂^*+x₂₂^*和要素供给量x₁^*+x₂^*，由它们可求出最大社会福利W^*。可以证明这样决定的资源配置是帕累托最优的。
〖参〗最大社会福利
　社会福利函数