最大值和最小值
最大值和最小值zuidazhi he zuixiaozhi
函数在定义域内或给定区间内的所有函数值中最大(或最小)的一个,叫做该函数在定义域内或给定区间内的最大(或最小)值.
例如,函数y=-2x2+3在定义域内的最大值是3.函数y=3x-2在区间[-2,2]上的最大值是4,最小值是-8.函数y=2x4在定义域内的最小值是0.
对于一些初等函数,常用的求最大(小)值的方法大致如下:
❶二次函数配方法:将二次函数y=ax2+bx+c
| (a≠0) |
| 的解析式配方,变为 |
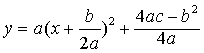 那么,当a>0时,函数有最小值(4ac-b2)/4a;当a<0时,函数有最大值(4ac-b2)/4a.例如,函数y=3x2-4x+5=3(x-2/3)2+11/3.当x=2/3时,y的最小值为11/3.
那么,当a>0时,函数有最小值(4ac-b2)/4a;当a<0时,函数有最大值(4ac-b2)/4a.例如,函数y=3x2-4x+5=3(x-2/3)2+11/3.当x=2/3时,y的最小值为11/3.❷不等式法:利用平均值不等式
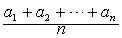
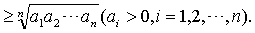 如果n个正数a1,a2,…an的和是定值,那么当a1=a2=…=an时,它
如果n个正数a1,a2,…an的和是定值,那么当a1=a2=…=an时,它| 们的积有最大值 |
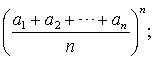
| 如果n个正数a1, |
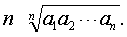 例如,函数y=2x2+1/x4,因为x2·x2·1/x4=1是定值,所以当x2=x2=1/x4,即x=±1时,y=2x2+1/x4有最小值3.
例如,函数y=2x2+1/x4,因为x2·x2·1/x4=1是定值,所以当x2=x2=1/x4,即x=±1时,y=2x2+1/x4有最小值3.❸判别式法:例如函数
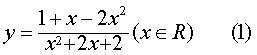
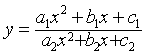
☚ 极值点 最大值 ☛
- 化毒饮子是什么意思
- 化民成俗是什么意思
- 化气是什么意思
- 化气丸是什么意思
- 化气丸是什么意思
- 化气丸是什么意思
- 化气丸是什么意思
- 化气兰是什么意思
- 化气兰是什么意思
- 化气兰是什么意思
- 化气四物汤是什么意思
- 化气散是什么意思
- 化气散是什么意思
- 化气汤是什么意思
- 化气汤是什么意思
- 化气汤是什么意思
- 化气沉香汤是什么意思
- 化气调经汤是什么意思
- 化水丹是什么意思
- 化水汤是什么意思
- 化水种子汤是什么意思
- 化水种子汤是什么意思
- 化流是什么意思
- 化浊汤是什么意思
- 化消极因素为积极因素是什么意思
- 化涎丸是什么意思
- 化涎半夏辰砂丸是什么意思
- 化涎散是什么意思
- 化涎饼子是什么意思
- 化清经是什么意思
- 化清肺汤是什么意思
- 化湿是什么意思
- 化湿是什么意思
- 化湿清火汤是什么意思
- 化湿饮是什么意思
- 化源是什么意思
- 化源是什么意思
- 化源是什么意思
- 化滞丸是什么意思
- 化滞丸是什么意思
- 化滞丸是什么意思
- 化滞丸是什么意思
- 化滞十香丸是什么意思
- 化滞和中汤是什么意思
- 化滞汤是什么意思
- 化滞汤是什么意思
- 化滞汤是什么意思
- 化滞汤是什么意思
- 化滞汤是什么意思
- 化滞调中汤是什么意思
- 化滞调中汤是什么意思
- 化漏汤是什么意思
- 化炎汤是什么意思
- 化爲乌有是什么意思
- 化物是什么意思
- 化狂丹是什么意思
- 化狂丹是什么意思
- 化理是什么意思
- 化生是什么意思
- 化生是什么意思