最大与最小

 至^①大无外，谓之大一；至小无内，谓之小一。(《庄子·天下》)
 

 【注释】　①至：即最。
 【译文】　最大的没有外边，最小的也没有里面。
 【评说】　惠施以此说明宇宙无论从大还是从小，或者说无论从宏观还是从微观讲都是无限的。“大一”是说整个空间大到无所不包，不再有外部；“小一”是说物质最小的单位，小到不可再分割，不再有内部。
 这里涉及两个抽象概念：“至大”和“至小”。最大的东西无限大，大到没有外边即“至大”;最小的东西无限小，小到没有内边即“至小”。但最大的和最小的都可以称为“一”,也就是说，“大一”和“小一”都是“一”。如果撇开它们在大小方面的区别，那么二者作为“一”是相同的。这表明，大和小的对立是相对的，它们之间是具有统一性的。

最大与最小Zuida yu zuixiao

这类问题涉及从小学到大学乃至最尖端数学研究各种不同深度的数学。小学中接触到的只是其中最浅显的内容。虽然如此，有关的问题对于学生体会数的大小概念，对于培养学生运算与比较的智巧， 仍是非常有益的。
例1（第一届华罗庚金杯赛复赛）:把14分成几个自然数的和，再求出这些数的乘积，要使得到的乘积尽可能大， 问这个乘积是几？
解：因为1与任何数乘积保持该数不变，故不会使乘积变大，这些自然数(和等于14)中不应有1。又任意大于4的自然数n，都可以排成两自然数的和(比如2和n-2)，它们的乘积大于n，因此这些自然数中不应有大于4的数。而2×2=2+2=4，故可以认为这些自然数或是3, 或是2。注意到2×2×2<3×3。因此把14写成3+3+3+3+2, 可使乘积3×3×3×3×2=162最大。对于其他自然数，也可照此办理，获得类似结论。如13分成3、3、3、4的和将使乘积3×3×3×4=108达到最大。
例2:从5、6、7、8、9五个数字中任取四个组成没有重复数字的四位数， 求其中能被3和5整除的最大和最小数。
解：依据题意及能被5整除的数的性质，可知这样的数个位上一定是5。其余3位数字之和被3除应余1(因为5≡2(mod3))。故能被3和5整除的四位数的4个数字必然是5、6、7、9、其中最大的数是9 765。
例3: 用20米长的篱笆围成的矩形院子， 最大面积是多少？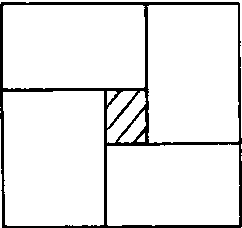
解：由题设，所围矩形长与宽之和为10米，4个这样的矩形可以一直一横拼接在一个边长为10米的正方形内， 如左图。因此4×矩形面积≤大正方形面积矩形面积≤1/4×100=25平方米。由此例， 可引伸出以下结论：
❶周长一定的矩形中，正方形面积最大，反过来，面积一定的矩形中， 正方形周长最小。

❷把一个正数分成两个正数之和，当两数相等时，乘积最大。
最大与最小的问题与规划统筹和最短线问题有密切关系。
例4:赵、钱、孙、李四人各拿一只水桶到同一水龙头接水， 水龙头的流量固定， 但各人的水桶容量不一，他们注满自己的水桶分别需要1、5、2、4分钟，怎样安排接水顺序， 可使四个人的总等待时间最省？
解：第一个人接水时，陪同等待的人最多，第二人次之，最后一人最小，为减少总的等待时间。应该这样安排：用时越多，陪同等待的人越少，因此，总等待时间最少的接水顺序是赵、孙、李、钱，此时的总等待时间为1×4+2×3+4×2+5×1=23分。由此例，可以引伸出以下结论：设a₁>a₂>…>an>0,b₁>b₂>…>b_n>0,c₁，…，c_n是a₁…，a_n的一个排列，则和式b₁c₁+b₂c₂+…+b_nc_n当c₁＝a₁,c₂＝a₂，…，c_n＝a_n时最大，而当c₁＝an, c₂＝an-₁, …， c_n＝a₁时最小。
借助这一结论，可以解决许多类似问题，例如，有A、B、C三个旅行团， 人数分别为20、30、50, 同时到达一宾馆， 服务台为每个团办理手续需要相同的时间。问怎样安排顺序可使全体旅客的总等待时间最少？据前述结论，此例的情形，排顺序的原则应为：人数多的优先。